Analiza grinzilor static nedeterminate 1

Exemple de soluții de probleme privind rezistența materialelor

Această pagină este un exemplu de rezolvare a problemei privind rezistența materialelor, care este necesar să se calculeze grinzi static nedeterminat, încărcate factorii de forță transversale. Calculele sunt definite mișcarea liniară a secțiunilor transversale fasciculului de-a lungul lungimii sale.

Rezultatele de calcul sunt decorate grinzi de îndoire Diagrama momentului și forțe de forfecare și mișcare liniară.

Elevii de specialități tehnice ale instituțiilor de învățământ superior ca o asistență metodologică oferită pentru a descărca variante gata făcute de lucrări de control asupra rezistenței materialelor (Mecanică aplicată). Exemplele prezentate de sarcini și soluțiile lor special concepute pentru studenții Universității Tehnice de Stat Altai.
Opțiunile de control lucrări pot fi descărcate în format Word pentru a revizui procedura de decizie sarcini, sau pentru imprimare și protecție (coincidență de opțiuni).

Analiza fasciculului nedeterminat static

Starea problemei:

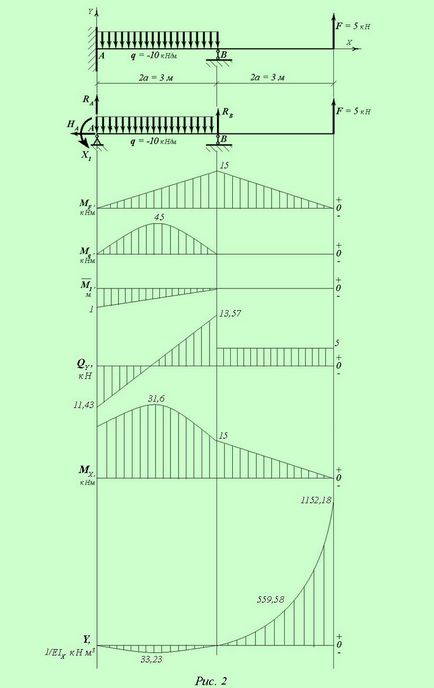
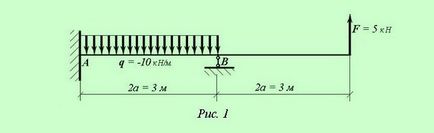
În fasciculul static nedeterminat având două picioare, terminații rigide A și suport pivotabil deplasabilă B. acționat de forțe externe: forța F și q sarcină distribuită (a se vedea figura 1 ..).

necesită:

Se determină reacțiile de sprijin, să construiască diagrame de forțe de forfecare, momente de îndoire și mișcare liniară.

Context:

• forță laterală F = 5 kN;
• distribuite q încărcare = -10 kN / m;
• valoare liniară = 1,5 m

• inițiale de coordonate sarcină distribuită ZQ = 0;
• sarcină distribuită se termină coordonate ZQ = 2a;
• ZF = 4 a - coordona aplicarea unei forțe concentrate;
• ZB = 2 a - coordonate Suportul.

Desenați o schemă de fascicul, în conformitate cu datele originale.
Anchorage situat la capătul din stânga al grinzii, în aceeași selectați originea.

Acest fascicul este nedeterminat odată static, deoarece reacțiile de suport are mai mult ecuațiile unității staticii. Prin urmare, utilizarea de metode statice pentru a determina factorii de forță necunoscute este imposibilă, ca o reacție de susținere este „extra“ și factorii de forță necunoscute este una mai mare decât ecuațiile de echilibru.

Pentru a rezolva problema folosind metoda Vereshchagin, de respingere „extra“ link-ul și înlocuirea acestuia cu o forță necunoscută X1. Pentru obligațiuni suplimentare poate adopta orice reacții de susținere, cu excepția care acționează longitudinal de reacție HA. pentru că fără ea, fasciculul nu va fi în măsură să mențină echilibrul.

Noi luăm pentru un cuplu suplimentar de obligațiuni reactiv MA. compune fascicul circuit echivalent (Fig 2), și scriere canonică putere metoda ecuației pentru sistem odată nedeterminat static:

Ca o conexiune în plus, am aruncat cuplul reactiv dat ecuația canonică este unghiul de rotație al fasciculului de origine t. E. În zona de ancoraj.

Pentru a calcula coeficienții ecuației canonice construct MF încărcăturii (la sarcini externe și F q) și unitatea de M1 (de la eforturile X1 = 1) momentul încovoietor și apoi le multiplică în conformitate cu metoda Vereshchagin (vezi. Fig. 2).

Prin produs Vereshchagin diagrame MF × M1 este egala cu aria diagramelor de marfă, înmulțită cu înălțimea diagramelor unitare luate în cadrul centrului de greutate al diagramelor de marfă. Astfel, cele două diagrame de linii nu ar trebui să aibă puncte de fractură, și cel puțin una dintre schemele ar trebui să fie liniară.
Pentru comoditatea calculelor MF și diagrame desface în foițe MQ. construirea lor pe diagrame separate.

Conform circuitului din Figura 2 coeficienții ecuațiilor canonice sunt definite prin formulele:

Înlocuim valorile obținute în ecuația canonică și de a găsi X1 forță necunoscută:

indeterminare static divulgate.
Negativă X1 valoarea forței arată că direcția acestei forțe este stabilită inițial fals, și, de fapt, este îndreptată spre partea opusă, adică momentul de încovoiere care acționează într-o etanșare strânsă a MA = - .. X1.

Acum, din ecuațiile staticii găsi reacții de sprijin ale fasciculului:

O valoare pozitivă a RB de reacție obținut indică faptul că direcția în diagrama din figura 1 este selectată corect.

Deoarece reacția a devenit pozitivă, direcția în diagrama este ales corect.
Ca o verificare a rezultatelor obținute formă ecuația de echilibru a forțelor care acționează asupra grinzii:

Pentru a construi diagrama de deplasare liniară Y (deformarea) este necesară pentru a determina valorile de 4 ... 5 secțiuni ale fasciculului.
În cazul nostru, este cunoscut faptul că mișcarea în suporturile A și B sunt egale cu zero, adică. E. YA = 0 și yB = 0.
Calculăm deviației la grinzi jumătatea deschiderii coordonate = a z1. z2 = 3 și în secțiunea extremă a fasciculului, unde forța aplicată F (z3 = 4 a).
Ecuațiile deviațiile aceste secțiuni au forma parametrii inițiali ai metodei:

Conform datelor estimate obținute construi diagrame ale forțelor laterale QY. incovoietoare MX și a murit Y (vezi. Fig. 2).