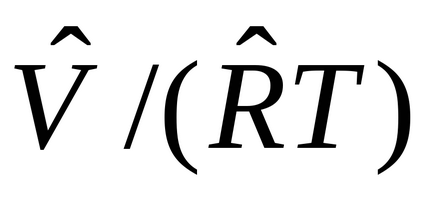Capitolul 2 din ecuația de stare a materiei
2.1. Ecuațiile termice si calorice de stat
Numărul total de stat vehicul ecuații termodinamice termică și este determinată de numărul de grade de libertate, și anume inclusiv impactul asupra vehiculului forțelor generalizate. Aceste ecuații sunt stabilite empiric sau este metodele fizicii statistice.
Pentru TC simplă (numărul de grade de libertate, N = 2), care are natură mecanică o singură forță generalizată - davlenier. parametruV extern conjugat. interacțiunea cu mediul este caracterizat de un singur parametru extern schimbare în reacție, (coordonata generalizată) - obemomV și temperaturoyT (parametru independent). Apoi, starea de echilibru a parametrilor interni: presiunea și energiyuU interne pot fi exprimate ca dependențe funcționale: p = p (V, T) - ecuația termică de stat și U = U (V, T) - ecuația calorică de stare.
Ecuația stare termică pentru un simplu TS poate fi reprezentat sub forma de conexiune: F (p, V, T) = 0. Această ecuație este stările termodinamice ale suprafeței sau suprafețelor. Pentru o ecuație a gazului ideal de stat este termic Clapeyron: pV = Mrt. în care R - constantă specifică a gazului.
Sostoyaniyaidealnogo gaz ecuația calorică poate fi obținută din legea Joule: „sistemyU internă energie termodinamic la T = const este independent de obemaV:
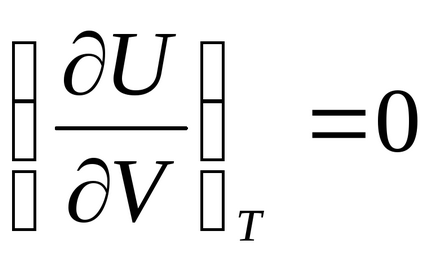
Diferențierea ecuația U = U (V, T), obținem:
,
unde
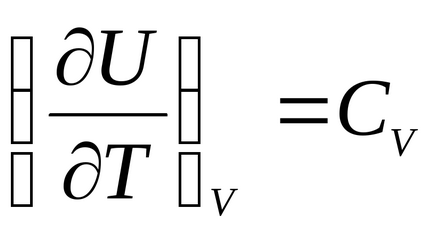
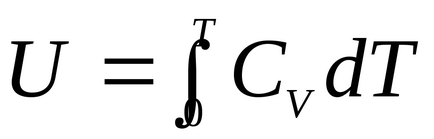
și anume energia internă a unui gaz ideal este o funcție a temperaturii:
.
Ecuația Caloric și termică a stării de gaz ideal poate fi obținut de la conceptele moleculare cinetice.
2.2. Ecuația termică a stat pentru un gaz ideal
Formal definit ca gazmozhno gaz ideal ascultare Clapeyron:
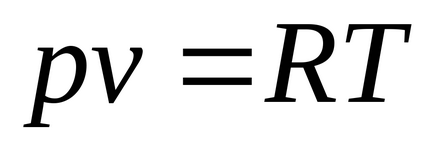
Din punct de vedere fizic un gaz ideal - un gaz a cărui extindere spațială molecule lipsite (volum de molecule de gaz în vasul - Vmol< , unde k = 1.380658 (12) 10 -23 [J / K] - constanta Boltzmann;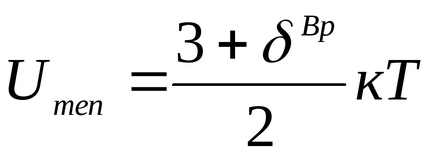
La 1 kg: pv = RT. în care R, J / kgK - constantă de gaz specific în funcție de tipul de gaz, p. Pa; v. m 3 / kg; T K.
La 1 mol de:
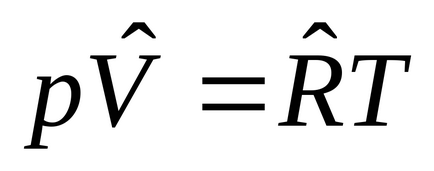

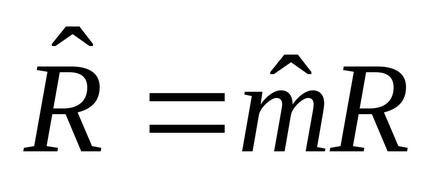

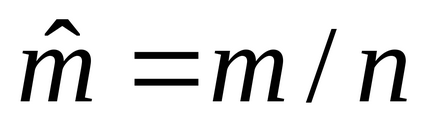
5. 1m 3:
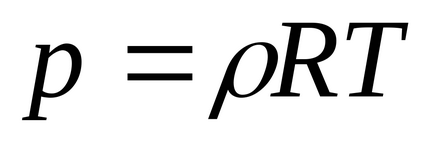
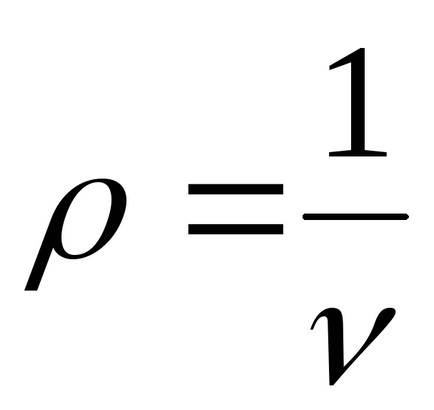
6. 1m 3:
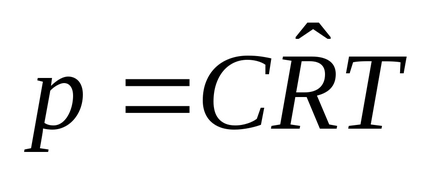
, unde
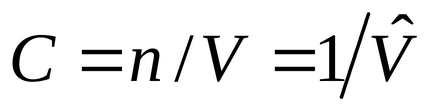
2.3. Ecuația stării termice pentru gazele reale
Forma specifică a ecuației termice depinde de starea de agregare și tipul de material. Este acum bine dezvoltat ecuația de stat doar pentru gazele reale. Pentru ecuația de stare a materiei condensate sunt extrem de rare, deoarece acestea nu sunt necesare pentru calcule practice.
Forma ecuația de stare pentru gazele reale este puternic dependentă de dimensiunea particulelor și structura acestora și natura interacțiunii dintre ele. Energia potențială interacțiune Udvuh moleculelor depinde de distanța dintre centrele lor -r. t.e.U = f (r). molecule de gaze reale au o dimensiune finită și sunt atrași unul de celălalt cu o forță care crește odată cu scăderea distanța medie dintre molecule, în contrast ideal kotorogoU gaz y (r) = 0.
Pentru calcule a potențialului energetic U este folosit mai ales de către Lennard-Jones:
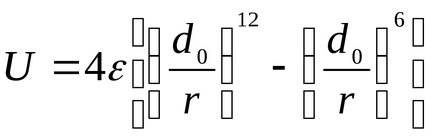
valorile denumiri

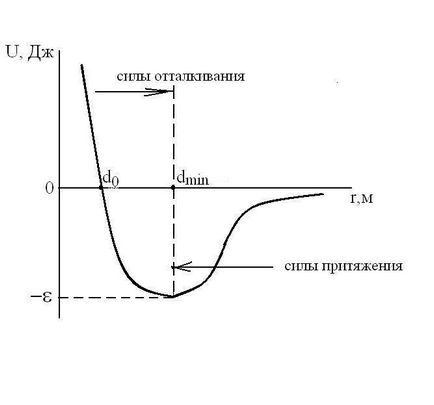
Forțele de interacțiune dintre moleculele
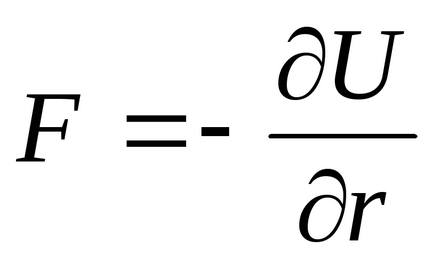
1 / r 6. Tăria și vzaimodeystviyaF
1 / r 7. Pentru rasstoyaniyr mici (cu molecule viguroase se apropie) U
Pentru comparație, observăm că pentru interacțiunea Coulomb potențialul U
1 / r 2. Astfel, forțele van der Waals scad odată cu creșterea rasstoyaniyar între particule este mult mai rapid decât forța Coulomb. Prin urmare, ecuația de stare pentru gazele reale de obicei, nu sunt potrivite pentru plasma. Pentru o ecuație stare de plasmă este derivată separat (Debye).
Forțele de interacțiune în funcție de distanța dintre particule (F = f (r)) sunt utilizate pentru a calcula coeficienții în diferite ecuațiile de stare și de gaz de plasmă reală.
Cea mai simplă ecuația de stare pentru gazele reale este ecuația lui van der Waals (1873.) (În prezent există mai mult de 150 de ecuații empirice). Această ecuație este de forma:
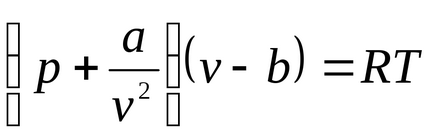
unde b - o corecție pentru volum molecular, a / v 2 - corectat pentru presiunea moleculară sau internă determinată de atracția reciprocă a moleculelor de gaz. Konstantya și b depind de tipul de gaz (de natura substanței).
Pentru lichide, această ecuație este puternic în contradicție cu datele experimentale. Această ecuație indică posibila existență a două faze și conduce la concluzia că există un punct critic. Dacă atributul parametrii p, T, v la parametrampk critică, Tc, vk la punctul critic al diagramei de fază și de a identifica
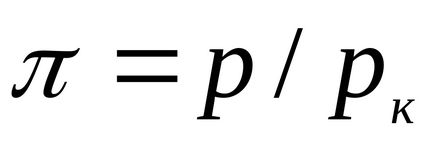
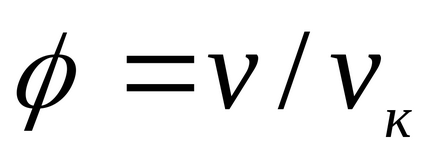
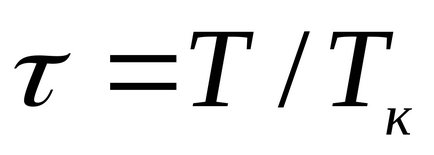
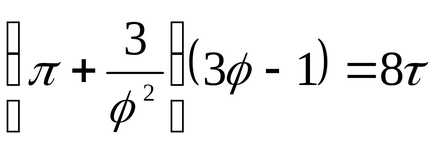
care exprimă legea statelor corespunzătoare.
Statele corespunzătoare sunt numite stări de diferite substanțe care au aceiași parametri enumerați



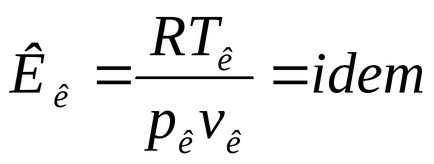
Pentru gaz vadervaalsovskogo Rk = 2.67.
Abaterea proprietăți de gaz real asupra proprietăților ideale de compresibilitate a gazelor poate fi caracterizată prin amploarea factorului de compresibilitate sau
Pentru un gaz ideal Z = 1. Pentru reală gazaZ ≠ 1. Magnitudinea factorului de compresibilitate depinde de presiunea, temperatura și tipul de gaz și poate fi mai mare sau mai mică decât unitatea în funcție de acești factori.
Ecuațiile de stare pot fi obținute pentru un gaz adevărat, având în vedere interacțiunea dintre particule. Aceste ecuații sunt numite ecuația virial de stat, care în V - formă sunt după cum urmează:
,
unde A (T) (T) C (T) - primul, al doilea și al treilea coeficienții virial, care depind de temperatură. P ecuatia virial are forma a forma:
Coeficienții A (T) în (T) C (T) asociat cu coeficienții A '(T), B' (T) C * (T).
Primul coeficientul A (T) este determinată de ciocnirile binare ale particulelor, al doilea coeficient B (T) - coliziuni triple de particule etc. coliziune simultană a număr mare de particule - este puțin probabil. Cel mai important rolul jucat de coliziuni de particule binare. În cazul în care contul lor de pe partea dreaptă a ecuațiilor virial sunt salvate doar doi termeni. Un exemplu al acestei ecuații este ecuația lui van der Waals. Coeficientul A (T) este determinată prin integrarea unui potențial de coliziune binar. Cu cât presiunea, trebuie luată în considerare este mai mare numărul de termeni pe partea dreaptă a ecuației virial.
ecuații de stare termică pentru diferitele substanțe sunt, de asemenea, stabilite de datele experimentale pentru compresibilitate Z = p