Care este forma canonică a ecuațiilor

Acasă | Despre noi | feedback-ul
Acest tip de ecuația standard convenționale, atunci când în câteva secunde, este clar modul în care aceasta definește un obiect geometric. În plus, forma canonică este foarte convenabil pentru multe sarcini practice. De exemplu, conform ecuației canonice a liniei „plat“. În primul rând, odată ce este clar că este drept, și în al doilea rând - elementar punctul vizibil deținute și vectorul de direcție.
Este evident că orice linie de ordinul 1 este o linie dreaptă. La etajul al doilea ne așteptăm nu este Doorman și companie mult mai diversă de nouă articole:
Clasificarea liniilor de ordinul al doilea
Folosind un set special de acțiuni, orice ecuație de ordinul a doua a liniei este una dintre următoarele tipuri:
(U - numere reale pozitive)
1) - ecuația canonică a elipsei;
2) - ecuația canonică a unui hiperbolă;
3) - ecuația canonică a parabolei;
5) - o pereche de linii care se intersectează;
6) - o pereche de linii imaginare care se intersectează (valabil numai cu punctul de intersecție la origine);
7) - o pereche de linii paralele;
8) - o pereche de linii paralele imaginare;
9) - o pereche de linii de potrivire.
Un număr de incompletitudinea cititorii ar putea avea impresia lista. De exemplu, la punctul №7 ecuație definește o pereche de linii. paralel cu axa. și se pune întrebarea: în cazul în care este ecuația. definește drept. paralel cu axa y? Răspuns: nu este considerat canonic. Drepte sunt același caz standard. Rotit 90 de grade, și o intrare suplimentară în clasificarea este redundantă, deoarece nu poartă nimic fundamental nou.
Astfel, există nouă și doar nouă tipuri diferite de linii de ordinul 2, dar, în practică, cele mai comune elipsa, hiperbola și parabole.
În primul rând, ia în considerare elipsei. Ca de obicei, mă concentrez asupra acelor momente care sunt de mare importanță pentru rezolvarea problemelor, și dacă aveți nevoie de o derivare detaliată a formulelor, dovedind teoreme, vă rugăm să consultați, de exemplu, la manualul Bazyleva / sau Atanasyan Alexandrov ..
Elipsă și ecuația canonică
Ortografie ... vă rugăm să nu repete greșelile unora dintre utilizatori Yandex care sunt interesați de „cum să construiască ellibz“ „Spre deosebire de elipsa oval“ și „elebsa excentricitate“.
Ecuația canonică are forma unei elipse. în cazul în care - numere reale pozitive, și. Însăși definiția elipsei Formulez mai târziu, iar acum este timpul pentru a lua o pauză de la magazinele vorbind și prevalența problemei pentru a rezolva:
Cum de a construi o elipsă?
Da, aici ia și doar trage. Setarea este comun, și o mare parte din studenții nu se face destul de competent cu desenul:
Construi o elipsă dată de ecuația
Decizie. În primul rând vom da ecuația la forma canonică:
De ce da? Unul dintre avantajele ecuației canonice este că vă permite să identificați instantaneu elipsei de top. care sunt în puncte. Este ușor de observat că coordonatele fiecăreia dintre aceste puncte satisfac ecuația.
În acest caz:
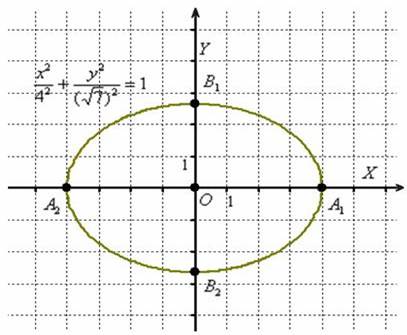
Segmentul numit axa mare a elipsei;
segment - axa minoră;
număr numit axa semi-majoră a elipsei;
Numărul - axa secundară.
în exemplul nostru.
Pentru a prezenta rapid aspectul unui anumit elipse este suficient să se uite la valoarea „a“ și „BE“ ecuația canonică.
Totul este bine, lin și frumos, dar există un avertisment: Am realizat cu ajutorul unor programe de desen. Și puteți face un desen folosind orice aplicație. Cu toate acestea, realitatea dură pe foaia de hârtie în carouri de masă, și pe mâinile noastre de plumb dansuri mouse-ului. Persoanele cu talent artistic, desigur, se poate argumenta, dar mouse-ul este, și tu, de asemenea (deși mai mici). A făcut cu bună știință omenirea a inventat o riglă, compas, echer și alte dispozitive simple pentru desen.
Din acest motiv, suntem puțin probabil să atragă cu precizie o elipsă, știind unele vârfuri. Cu toate acestea bine, în cazul în care elipsei este mic, de exemplu, cu axele. Alternativ, scala poate fi redusă și, în consecință, dimensiunile de desen. Dar, în general, este foarte de dorit să se găsească puncte suplimentare.
Există două abordări pentru construirea unei elipse - o geometric și algebric. Compass-construcție și-dreptar nu-mi place, din cauza nu foarte scurt a algoritmului și o dezordine întinderi. În caz de urgență, vă rugăm să consultați cartea, dar în realitate este mult utilizarea mai rațională a mijloacelor algebra. Din ecuația elipsei în proiectul exprimă rapid:
În continuare, ecuația este împărțit în două funcții:
- definește arcul superior al elipsei;
- definește fundul arcului elipsei.
Orice elipsă este simetrică în raport cu axele de coordonate, precum și în ceea ce privește originea. Și e bine - simetria este aproape întotdeauna un vestitor de freebies. Este, evident, suficient pentru a face față cu primul trimestru al coordonate, deci trebuie să funcționeze. Acest lucru conduce la găsirea punctelor suplimentare cu abscise. Nastukaem trei SMS-uri de pe calculator:
Desigur, frumos și faptul că, dacă face o greșeală gravă în calcule, este imediat clar în curs de construcție.
Notă punctul de desen (roșu), punctele simetrice pe alte arce (de culoare albastră) și să se alăture cu acuratețe linia de întreaga companie:
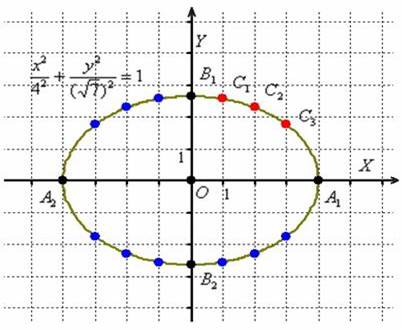
Schița inițială este mai bine trage un strat subțire este subțire, și apoi adăugați creion de presiune. Rezultatul ar trebui să fie o elipsă demn. Apropo, nu vă place să știu ce fel de curba?