Centrul de masă al sistemului mecanic
momentul Polar este suma produselor de puncte de masă ale sistemului la distanța lor de la pătrat la centru (în acest caz, de la origine):
Momentele de inerție măsurate în kg # 8729; m 2.
Din expresiile (3.13) și (3.14) rezultă că
Un moment de inerție centrifugal egală cu suma algebrică a produselor din masa fiecărui punct din sistemul produsul de coordonatele sale corespunzătoare:
Dacă momentele centrifugale cu privire la orice sistem de coordonate sunt egale cu zero, atunci axa sistemului numit axele principale de inerție la origine. Dacă axa trece prin centrul de masă, numită axa centrului.
Momentul de inerție al corpului în raport cu o axă predeterminată, cum ar fi axa Ox. Acesta poate fi reprezentat ca produs al greutății corporale prin pătratul valorii liniare numită rază de inerție în raport cu axa:
unde m - greutatea corporală; # 961; x - inerție raza în raport cu axa Ox.
Relația dintre momentele de inerție în raport cu axele paralele z și una dintre care axa trece prin centrul de masă al corpului C (fig. 3.6), setează teorema lui Huygens-Steiner.
Huygens-Steiner teorema. Momentul de inerție al sistemului mecanic în raport cu orice axă este momentul său de inerție în raport cu axa paralelă care trece prin centrul de masă al sistemului, plus produsul dintre masa m a sistemului pe pătratul distanței dintre axele d:
Dovada. Lăsați sistemul să aibă două axe de coordonate rectangulare paralele între ele și Oxyz (fig. 3.6). Punctul C este centrul de masă. Prin definiție, momentele de inerție axial sunt de forma
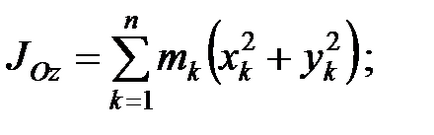
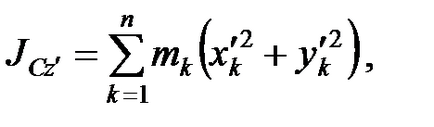
unde mk - punctul de masă Mc. și - coordonatele acestui punct în raport cu un sistem de coordonate Oxyz și respectiv. Aceste coordonate sunt legate prin transfer paralel
Înlocuind aceste valori în expresia coordonată de inerție joz și după transformare obține
Noi luăm în considerare faptul că
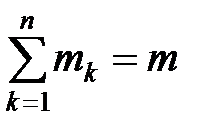
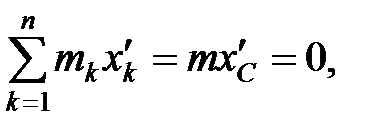
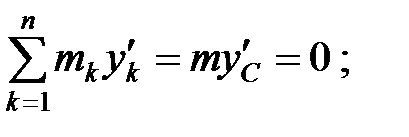
unde d - distanța dintre axele Oz și
În cele din urmă, avem ceea ce ne-am dorit să dovedească.
Din teorema care pentru o multitudine de axe paralele este cel mai mic momentul de inerție în jurul axei centrale.