Convexitatea, concavitatea graficul funcției, punctul de inflexiune
Caracteristicile de studiu în concavitate și convexitate poate fi o sarcină separată și una dintre etapele unei investigații complete a funcției și construirea programului său. Convexitate și funcția concavitate are loc numai la un anumit interval, și cu care sunt asociate definițiile chestii enumerate.
Programeaza o funcție convexă diferențiabilă este numit în intervalul] a. b [, dacă în acest interval este situat sub fiecare tangent sale (Fig. 1).
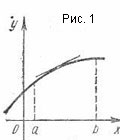
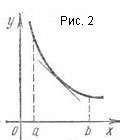
Grafic funcție diferențiabilă concavă numită în acest interval este situat deasupra fiecărei tangent sale (fig. 2).
Teorema (concavitate suficientă sau grafică convexitate). Dacă funcția f (x) la toate punctele din intervalul] a. b [
curba y = f (x) este concavă în acest interval; dacă
la toate punctele din intervalul] a. b [, curba convexă în acest interval.
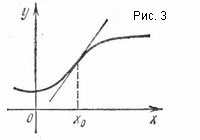
punct continuu funcție grafic, la care se schimbă în concavitatea sau convexitatea dimpotrivă, se numește punct de inflexiune.
Din definiția rezultă că o parte a punctului de inflexiune al curbei este situat la o tangentă, pe de altă parte - peste el, sau vice-versa. Prin urmare, un punct de inflexiune pe un grafic realizat pentru a arăta un segment al tangentei la acest punct care se intersectează curba (fig. 3).
Teorema (o indicație suficientă a existenței punctului de inflexiune). Dacă punctul funcția f (x) este prima derivată și derivata a doua în acest punct este egal cu zero sau nu există, și, în plus, pe care trece prin schimbări semn,
este punctul de inflexiune al graficului y = f (x).
Astfel, pentru a investiga natura convexitatea curbei y = f (x). pentru a găsi punctele în care fie nu există, și apoi, folosind un criteriu suficient pentru a investiga semne de al doilea derivat de pe partea stângă și dreaptă a fiecărui posibil punct de inflexiune (doar punctul extremum ca determinată a primei derivate).
Exemplul 1. Găsiți punctul de inflexiune și de a stabili natura convexitatea graficului funcției.
Decizie. Funcția este definită pentru. Și derivații săi. Găsiți posibile puncte de inflexiune. Presupunând că avem t. E., presupunând că vom obține.
Cu toate acestea, punctele și nu sunt incluse în domeniul unei funcții date, astfel că poate avea doar un singur punct de inflexiune la. Noi investigăm semnele derivata a doua în jurul punctului. Luând interval punct, obținem, ca având punctul interval au. În consecință, în partea stângă a curbei este convexă. și pe dreapta - concav. Prin urmare, atunci când funcția programul are un punct de inflexiune.
Graficul acestei funcții - Fig. de mai jos.
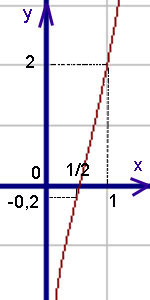
Exemplul 2. Găsiți punctul de inflexiune, natura convexitate și concavitate și complot funcția.
Decizie. Funcția este definită pentru. Și derivații săi. Aici, și în, cu și sub. În consecință, în partea stângă a curbei este concavă. și pe dreapta - convexe. și anume - punctul de inflexiune al graficului.
Graficul acestei funcții - Fig. de mai jos.
Exemplul 3. Testul pentru funcția convexitate, concavitate și punctul de inflexiune.
Decizie. Găsim derivata a doua :. Din ecuația obținem un punct critic :. Examinarea semnului din cartier obține .. În partea stângă a punctelor (convexe), precum și dreptul - (concavitatea), adică, punctul este punctul de inflexiune al funcției.
Graficul acestei funcții - Fig. de mai jos.