Cum de a găsi suma vectorială

Adăugarea de vectori ai regulii triunghiului. Fie a și b - două nenulă vector. Amână un vector din punctul O, și reprezintă ea până la sfârșitul litera A. OA = a. Amânată de la A vector b, și reprezintă ea până la sfârșitul literei B. AB = b. Un vector pornind de la punctul O și punctul final B (S = s) se numește suma vectorială a și b, și scrie c = a + b. Pe vector cu spune că este derivată dintr-o combinație de vectori a și b.

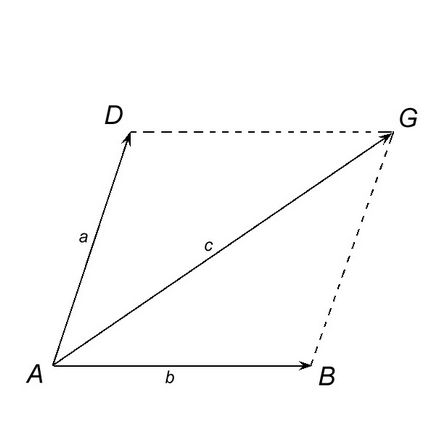
Suma a doi vectori coliniare a și b pot fi construite prin regula, numita regula paralelogramului. Amînarea punctului A = b vectorii AB și AD = a. După sfârșitul vectorului și trage o linie paralelă cu vectorul b, iar prin capătul vectorului b - o linie dreaptă paralelă cu vectorul a. Fie C - punctul de intersecție al liniilor construite. Vector AC = c - sumă a vectorilor a și b.
c = a + b.

Vector, vectorul și opusul este numit un vector, denumit - și astfel încât suma unui vector și vectorul s este egal cu vectorul de zero:
a + (-a) = 0
Vector opus vectorului AB, denumit BA:
AB = AA + VA = 0
Vectorii opuse nenuli au lungimi egale (| a | = | -a |) și în direcții opuse.

Vectorul sumă a și b vector opus diferenței vector a doi vectori, menționate ca - b, adică vectorul a + (-b). Diferența dintre doi vectori a și b denota a - b.
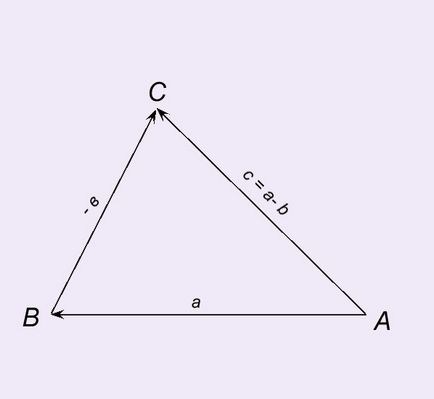
Diferența dintre doi vectori a și b pot fi obținute utilizând o regulă triunghi. Amînarea punctul A și vectorul. AB = a. De la sfârșitul vectorului AB amâne vectorul BC = -b, vectorul AC = c - diferența vectorilor a și b.
c = a - b.

operațiune Proprietăți de adăugare vector:
1) proprietate vector de zero:
0 = a + a;
2) adăugarea asociativitatea:
(A + b) + c = a + (b + c);
3) comutativitate:
a + b = b + a;