Cum de a găsi zona unei formule de bază triunghi echilateral

Calculul suprafeței triunghiului în acest caz va fi efectuată în conformitate cu formula:

Este ușor să ieși din asta, care este cunoscut pentru o formă arbitrară cu trei laturi. Doar în formula ar trebui să ia în considerare faptul că toate partidele din triunghiul sunt egale.

Mai precis, necesitatea Heron formula: S = √ (p (p-a) (p-b) (p-c)). Valoarea pentru jumătate de perimetrul triunghiului echilateral este egal cu 3a / 2. Astfel, fiecare suport sub rădăcină obținem o expresie ((3a / 2) - a). Va după convertirea la un / 2.

Deoarece cele trei paranteze, atunci această expresie va fi al treilea grad. Deci, acesta este convertit la un 3/8.

Ea trebuie încă să fie multiplicat cu jumătate de perimetru, care este definit ca suma dintre laturile împărțit la 2 pentru a se obține o expresie: 3a 4/16. După ce a luat rădăcina pătrată este doar o expresie a voinței, care este dat în prima formulă pentru aria unui triunghi echilateral.

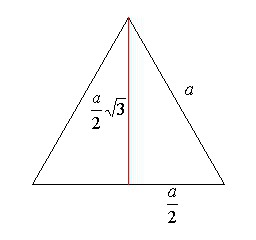
Prin urmare, nu este nevoie să memoreze o mulțime de formule. Puteți aminti doar unul - Gerona. Din aceasta printr-un simplu transformări matematice obținute toate celelalte, de exemplu, un triunghi echilateral.

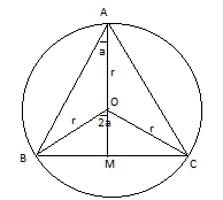
Formula 2: având o rază de cerc înscris

Această expresie este foarte similar cu precedentul record. Dar există diferențe semnificative: utilizează o literă diferită, iraționalitatea unui lucru al numitorului, a existat un factor de 3 și a dispărut figura 4. În general, este ușor de reținut.

Această formulă este, de asemenea, ușor pentru a obține din ceea ce este dat pentru un triunghi arbitrar. Acesta este înmulțită cu suma razei de părți și este împărțit la 4. Din moment ce părțile au aceeași valoare ca suma se înlocuiește cu 3a. Acum aveți nevoie pentru a elimina „o“ de a avea doar o valoare de rază. Acest lucru va necesita o expresie în care partea este împărțit de produsul de 2 și sinusul unghiului de partea opusă. Deoarece unghiul este 60º, valoarea sine este √3 / 2. Apoi laturile exprimate prin raza după cum urmează: a = √3R. Dupa o simpla transformare poate veni la expresia pătrat, care a fost dat la început.

Formula 3: cerc dat circumscrisă și raza

Este foarte similar cu primul. Numai în numărător apare numărul 3 și scrisoarea a fost schimbat la R.

Deoarece raza dublă față de cea care a fost discutat în paragraful precedent, este clar modul în care se obține. Este pur și simplu pus în r R / 2. Și transformările necesare.

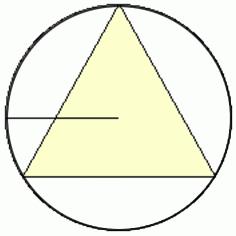
Prin urmare, formula nu poate aminti. Doar ține cont de raportul dintre razele cercurilor inscriptionare circumscrise în jurul unui triunghi echilateral.

Formula 4: cunoscut înălțime

În acest caz, aria unui triunghi echilateral este egal cu:

Pentru a înțelege modul în care aceasta este o astfel de formulă, din nou, trebuie să folosim comune pentru toate triunghiuri. Ea arata ca o lucrare de mână la înălțimea și ½. Acum, pentru a găsi zona unui triunghi echilateral, este necesar să se amintească sau să retragă o expresie matematică pentru înălțimea.

ușor de a învăța, dacă vom folosi faptul că înălțimea unei forme de triunghi dreptunghic. Aceasta înseamnă că înălțimea poate fi găsit ca piciorul - din teorema lui Pitagora. A doua etapă va fi egală cu jumătate din latura, deoarece înălțimea este, de asemenea, valoarea mediană (aceasta este o proprietate cunoscută dintr-un triunghi echilateral). Apoi, înălțimea este definită ca fiind rădăcina pătrată a diferenței dintre cele două pătrate. Originea "o", iar al doilea "a / 2". După erecție rămâne în al doilea grad și rădăcină extractului: n = (√3 / 2) * a. Din ea a = 2N / √3. După înlocuind-o în formula de bază pentru toate triunghiurile obținem expresia, care este listat la începutul acestei secțiuni.

Stare. Se calculează aria unui triunghi echilateral, în cazul în care se știe că partea sa este de 4 cm.

Decizie. Din moment ce știm valoarea cifrelor de partid, este necesar să se utilizeze prima formulă.

În primul rând, trebuie să pătrat numărul 4. Din această acțiune va număra 16. Acum, acesta este redus la Cvartetului, la numitor. Și, în sfârșit, în numărătorul este 4 și √3, iar numitorul este egal cu unu, ceea ce înseamnă că nu se poate scrie pur si simplu. Acest rezultat, care urma să fie găsit în problema.

Raspuns: 4√3 cm 2.

Stare. Toate laturile unui triunghi echilateral sunt egale 2√2 dm. Se calculează suprafața sa.

Decizie. Argumentele sunt aceleași ca și în prima problemă. Numai valoarea partea pătrat va fi diferit. Este necesar să se construiască separat etapa a doua 2 și iraționalitate. Iar rezultatul este: 4 * 2 = 8. După reducerea cu numitorul este √3 și 2 în numărătorul și numitorul dispare.

Raspuns: 2√3 dm 2.

Stare. Triunghiul echilateral inscripționată cerc, raza de 2,5 cm. Este necesar să se calculeze aria triunghiului.

Decizie. Pentru a calcula nevoia de a utiliza valoarea dorită a doua formulă.

În primul rând, aveți nevoie de raza la pătrat. Ia-6,25. Apoi, această valoare trebuie să fie multiplicată cu 3. Rezultatul acestei acțiuni va fi numărul 18.75. Dar acest lucru nu este valoarea finală: acesta va fi un factor √3, care este prezent în formula utilizată.

Raspuns: 18,75√3 cm 2.

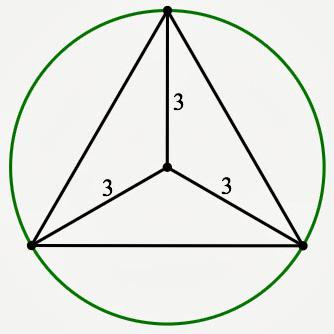
Stare. Este necesar să se determine care este aria unui triunghi echilateral, dacă știm înălțimea - 3 dm.

Decizie. În mod firesc, necesitatea de a selecta a patra formulă. Cu acesta, cel mai simplu mod de a găsi răspunsul la această problemă.

Unul are nevoie doar de la numărul 3 pătrat, adică înălțimea care va da valoare 9. Apoi împărțiți-l de √3, stând în formula.

Deoarece matematica nu se obișnuiește să părăsească iraționalității în numitorul răspunsul, atunci ai nevoie pentru a scăpa de ea. Pentru aceasta fotografie 9 / √3 trebuie să fie multiplicate cu fracțiunea cu aceeași numărătorul și numitorul, și anume √3 / √3. Din această acțiune apare în valoarea numărătorul 9√3, iar numitorul va apărea numărul 3.

Această fracțiune poate fi și trebuie redusă cu 3. Acesta este rezultatul final.

Raspuns: Zona - 3√3 dm 2.

Stare. Dan triunghi echilateral a cărui suprafață este egală cu 27 cm 2. Din această valoare, trebuie să știți lungimea figurii.

Decizie. Din moment ce aceasta este o parte, prima formulă este adecvată. Din aceasta puteți obține imediat o expresie matematică, care va determina direcția triunghiului.

În acest scop, zona ar trebui să fie înmulțită cu patru și împărțit la rădăcina pătrată a trei. Deci, pentru a obține valoarea pentru partid în pătrat. Pentru a obține doar direcția în care trebuie să ia o rădăcină. Expresia pentru partea va fi: a = 2 * √ (S / √3).

Având în vedere că zona este cunoscută, este posibil să se înceapă imediat de calcul. Expresia radicala arata ca privat 27 și √3. Pentru a scapa de iraționalitate la numitor. Will 27√3, împărțit la 3. După reducerea numitorul este 1, care nu se pot scrie, iar numărătorul este 9√3.

Următorul pas va fi de a extrage rădăcina pătrată a expresiei rezultată. Primul factor dă valoarea 3. Dar al doilea - √3 - are nevoie de atenție. Pentru a simplifica sarcina, puteți elimina aceste rădăcini și valori rotunjite.

√3 = 1,73; Acum, din nou și pentru a obține extract de rădăcină de 1.32.

Rămâne doar să-l înmulțim cu 2 și pentru a obține rezultatul dorit.

Raspuns: Partidul este egal cu 2,64 cm.