deformare solid

Avand in vedere mecanica corpului rigid, am folosit conceptul unui corp rigid. Cu toate acestea, în natură nu există nici corpuri rigide, din moment ce tot corpul real, de către forțele schimbă forma și mărimea lor, adică. E. deformeaza.

Deformarea se numește elastică în cazul în care, după încetarea forțelor externe, organismul are dimensiunea inițială și forma. Deformații că sohranya-

Ele sunt în organism după încetarea forțelor externe, sunt numite de plastic (sau rezidual). Deformarea de fapt, al doilea corp este întotdeauna de plastic, deoarece acestea sunt după încetarea forțelor externe nu vor dispărea complet. Cu toate acestea, în cazul în care deformările reziduale sunt mici, ele pot fi ignorate și luate în considerare în sus-THER tulpina pe care o vom de-lat.

Elasticitatea se dovedește că toate tipurile de suprasolicitare (tensiune sau compresiune, forfecare, încovoiere, torsiune) poate fi redusă la loc simultan la întindere deformare-conductiv sau FAS-ment și forfecare.

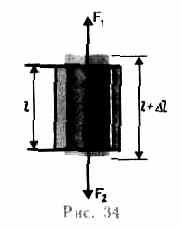
Să considerăm o tijă omogenă de lungime l și aria secțiunii transversale S (fig. 34), ale cărei capete sunt atașate de-a lungul axelor îndreptate forțează f1 sale și F2 (F1 = F2 = F), prin care Sr-zhnya schimbă lungime prin Soacra. Natural, dar care Soacra la întindere și compresiune pozitivă - negativ.

Forța care acționează asupra unui spectacol de mila unitate-OLP la secțiunea transversală se numește pe-conjugat:

În cazul în care forța este dirijată de-a lungul normalei la suprafață este, găurile tensiune formală-numit, în cazul în care la o tangentă la suprafața în - tangențială.

O măsură cantitativă a gradului de deformare-conductive, corpul de testare este relativă sale deformare infor. Astfel, modificarea relativă în lungime a tijei-HN (tulpina longitudinală)

e = Soacra / l. (21,2) transversală în raport de întindere

e „= Dd / d, unde d - diametrul tijei.

Deformarea e, e „sunt întotdeauna semne de timp-Nye (Soacra cu tracțiune pozitivă, un anunț negativ de compresie Soacra negativ, un anunț de pozitiv). Din experiență rezultă relația dintre e și e „:

în cazul în care m - coeficient pozitiv pentru agățat pe proprietățile materialului-mi-numitul raport Poisson.

Fizicianul englez Robert Hooke (1635- 1703) a stabilit experimental că pentru deformări mici în raport UD-Lynen e și stresul e drept pro-proporțional între ele:

în care coeficientul de proporționalitate E este modulul lui Young. De la tine-expresia (21.3) arată că modulul lui Young este determinată de stresul cauzat de o alungire de una. Formulele (21,2), (21.3) și (21.1), vă urmează că

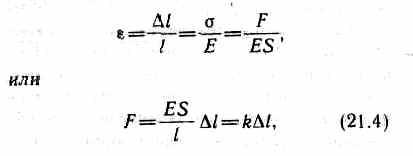
unde k - coeficientul de elasticitate. Expression-set (21.4) stabilește, de asemenea, legea Hooke, potrivit căreia alungirea co-web când deformarea elastică este proporțională forță care acționează asupra tijei.

Deformarea solide se supună legii lui Hooke până la un punct. Relația dintre tulpina și stres pre-reprezentate sub forma diagramei tensiune TION, considerăm calitatea eșantionului metalic (Fig. 35). Figura arată că o dependență liniară a lui (e), set Hooke se realizează

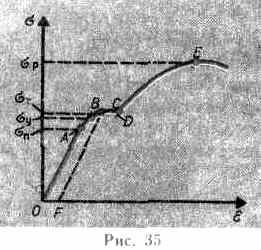
numai în limite foarte înguste, la așa-linking la limita de proporționalitate (Sn). Odată cu creșterea în continuare a deformării elastice de tensiune zheniya chiar (deși în dependență de s (e) nu mai este liniară) și la elastic pre-caz (Sy) rezidual de deformare-TION nu apare. Dincolo de limita de elasticitate în organism având tulpina reziduală și un grafic care descrie corpul pentru a reveni la starea inițială după Terminată scheniya forța, reprezentată de un nu-Cree urlând IN, și paralel cu acesta - CF. Tensiune de tensiune la care o tulpină reziduală apreciabil (

= 0,2%), INDICA numitul randament stress (SY) - punctul C de pe curba. În CD-ul tulpina crește fără o creștere a stresului t. E. corp ca „curge“. Această zonă este numită zona de curgere (sau zone de deformare plastică). Mate-riali, care produc suprafață semnificativă numit vâscos, pentru care ea este practic absentă - sfărâmicios. La tensiunea suplimentară (în afara punctului D) are loc distrugerea corpului. Tensiunea maximă produsă în organism la fractură este numită o rezistență pre-rupere (sp).

Figura tensiuni pentru solide reale depinde de diverse facto-șanț. Același organism rigid poate printr-o acțiune scurtă a forțelor se manifestă ca fragilă și cel lung, dar puterea slabă curge.

Uprugorastyanutogo calcula potențialul energetic (comprimat) tija Koto-paradisul egal cu lucrul mecanic efectuat de forțele externe, în timpul deformării:

unde x - rod lungirea absolută, care variază în timpul deformării de la 0 la Soacra. Conform legii lui Hooke (21,4), F = kx = ESX / l. prin urmare

t. e. potențială tija uprugorastyanutogo energie proporțională cu Quadra-deformare (Soacra) 2.

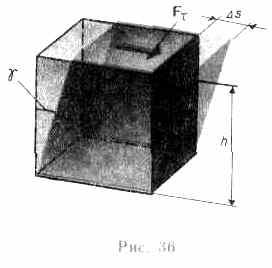
Forfecare deformare mai ușoară viespe-există luând o bară având o formă dreptunghiulară și atașați paralelipiped la ea forța Ftau (Fig.36), tangenta la suprafața sa (partea de jos a barei este atașată fix). shear relativă tulpina definită determinată de formula

unde Ds - corp de deplasare absolut straturi paralele în raport unul cu altul; h - distanța dintre straturile (pentru mici yr TGG pescuit »g).

• Care este momentul de inerție al corpului?

• Care este rolul momentului de inerție în mișcare de rotație?

• Care este formula pentru energia cinetică a unui corp de rotație în jurul unei axe fixe, și cum

• Ceea ce se numește momentul unei forțe cu privire la un punct fix? în raport cu Fixe

axa? Cum este direcția momentului de forță?

• Afișaj și specificați ecuația dinamică a mișcării de rotație a unui solid.

• Care este momentul cinetic al unui punct material? Solid State? După cum este stabilit de direcția momentului unghiular?

• Care este natura fizică a legii conservării momentului cinetic? În unele sisteme se execută o mișcare? Dă exemple.

• Cum proprietățile de simetrie ale spațiului este determinată de validitatea legii conservării momentului cinetic?

• Care sunt axa libere (axa principală de inerție)? Care dintre ele sunt stabile?

• Care este giroscopul? Care sunt principalele sale caracteristici?

• Formulați legea lui Hooke. Când a fost corect?

• Dă calitative diagrama explicație stres s (e). Ce este dincolo de proporțională-ționalitate, elasticitate și rezistență?

• Care este sensul fizic al modulului lui Young?

4.1. Cu un nivel de planurile înclinate simultan începe să se rostogolească fără glisante cilindru solid și o sferă de aceeași masă și aceeași raze. Definiți: 1) relația dintre viteza cilindrului și bilă la acest nivel; 2> relația lor la momentul de timp nici unul. [1) 14/15; 2) 14/15]

4.2. Spre omogenă solidă raza discului jantă R = 0,5 m aplicată constant evaluate la valoarea forței tangentă F = 100 H. Prin rotirea discului pe ea acționează cuplul de frecare M = 2H • m. Pentru a determina masa m a discului, în cazul în care este cunoscut faptul că accelerația unghiulară este constantă și egală cu 12 rad / s 2 [32 kg]

4.3. După fixarea unității sub forma unui cilindru solid de o masă omogenă m = 1 kg-ta perekinu fir fără greutate, capetele cărora mase m1 = 1, m2 = 2 kg corp atașat. Prenil Neglijând frecare în axa bloc pentru a defini: 1) accelerarea mărfurilor; 2) raportul T2 / T1 forțe asupra firului de racordare. [1) 2,8 m / s 2; 2) 1.11]

4.4. Viteza de rotație al roții, momentul de inerție este de 2 kg • m 2 rotative ravnozamedlenno la frânarea, cu timpul t = 1 min a scăzut de la n1 = 300 rot / min până la n2 = 180 rot / min. Definiți: 1) e accelerația unghiulară a roții; 2) de frânare vigoare momentul M; 3) Activitatea forței de frânare. [1) 0,21 rad / s 2; 2) 0,42 N • m; 3) 630 J]

4.5. Masa individuală m = 80 kg în picioare pe o muchie orizontală a masei platformei M = 100 kg de rotație prin inerție față de axa verticală fixă ​​cu n1 frecvență = 10 min -1. se deplasează spre centrul său. Presupunând disc uniform platformă rotundă și umană - masa unică AF-TION, determină frecvența cu care n2 se va roti apoi platforma. [26 min -1]

4.6. Se determină tija de aluminiu atunci când elongația sub tensiune de lucru 621 cheltuită J. Stem 2 m lungime, o secțiune transversală de 1 mm 2 Modulus Young pentru aluminiu E = 69 GPa.

* S. Poisson (1781 - 1840) - om de știință francez-cer.

** T. Jung (1773-1829) - om de știință britanic.