Derivata funcției în punctul

Cum de a găsi derivata funcției în punctul? Din formularea ar trebui să fie două puncte evidente ale acestei sarcini:

1) Este necesar să se găsească derivatul.

2) Este necesar să se calculeze valoarea derivatului la un anumit punct.

Se calculează derivata unei funcții într-un punct

Referință: Următoarele proceduri se referă la caracteristici echivalente: este convenabil să desemneze funcția de „y“ în unele locuri de muncă, iar unele prin „eff X“.

În primul rând, vom găsi derivat:

Din fericire, mulți s-au adaptat pentru a găsi acești derivați pe cale orală.

În a doua etapă se calculează valoarea derivatului de la punctul:

Un mic exemplu de un warm-up pentru autodeterminare:

Se calculează derivata unei funcții într-un punct

Soluții complete și răspunsuri la sfârșitul lecției.

Necesitatea de a găsi derivat într-un punct are loc în următoarele sarcini: construirea unei tangenta la graficul funcției (paragraful următor), funcția de cercetare pe extremă. Studiu privind inflexiunea funcție a graficului. studiul complet al funcției și altele.

Dar având în vedere locul de muncă are loc în activitatea de control în sine. Și, de regulă, în astfel de cazuri, da o funcție destul de complexă. În acest sens, ia în considerare mai multe două exemple.

Se calculează derivata funcției în punctul. În primul rând, vom găsi derivat:

Derivata, în principiu, este găsit, și este posibil să se înlocuiască valoarea dorită. Dar ceva care nu se simt cu adevarat ca faci. Exprimarea este foarte lung, iar valoarea „X“ în fracțional nostru. Așa că încercăm să simplifice derivatul nostru. În acest caz, vom încerca să aducem la un numitor comun în ultimele trei termeni:

Ei bine, destul de o altă problemă. Se calculează valoarea derivatului de la punctul:

În cazul în care nu înțeleg cum să găsească derivatul, du-te înapoi la primele două lecții ale subiectului. Dacă întâmpinați dificultăți (lipsa de înțelegere), cu tangenta cu arc și valorile sale, asigurați-vă că pentru a verifica programele și proprietățile materialelor metodice ale funcțiilor elementare - ultimul paragraf. Pentru că arctangents la vârsta de student au încă suficient.

Se calculează derivata funcției în punctul.

Acesta este un exemplu pentru soluțiile independente.

Ecuația tangentei la graficul funcției

Pentru a consolida secțiunea anterioară, considerăm problema găsirii funcției tangentă kgrafiku în acest moment. Această sarcină ne-am întâlnit la școală, și, de asemenea, are loc în cursul matematici superioare.

Luați în considerare „demo“ cel mai simplu exemplu.

Ecuația tangentei la graficul funcției în punctul cu abscisa. Eu dau imediat o soluție grafică completă a problemei (în practică, de a face acest lucru, în cele mai multe cazuri nu este necesar):

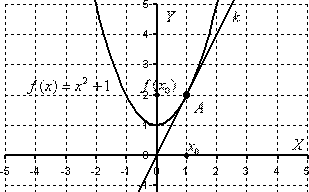
O definiție riguroasă a tangentă este dată prin determinarea funcției derivat. dar vom stapani partea tehnică a întrebării. Cu siguranță aproape toată lumea în mod intuitiv că această tangentă. În cazul în care pentru a explica „pe degete“, tangenta la graficul funcției - o linie dreaptă. care se referă la graficul unui singur punct. În același timp, toate punctele din jurul liniei sunt situate cât mai aproape posibil de graficul funcției.

În cazul nostru: tangenta (notație standard) pentru funcțiile grafice într-un singur punct.

Și sarcina noastră este de a găsi ecuația liniei.