Determinarea rangului unei matrice

Pentru a lucra cu conceptul de rangul unei matrice, avem nevoie de informații de la subiect „adăugirile algebrice și minori. Tipuri de minori și cofactori.“ În special, acest lucru se aplică termenul „minor al matricei.“ ca rangul matricei să devină detecta este prin minori.

Rangul unei matrice se numește ordinul maxim al minorilor sale, printre care există cel puțin un non-zero.

Echivalent matrice - matrice ale cărei rândurile sunt egale.

Să ne explicăm mai detaliat. Să presupunem că printre minori de ordinul al doilea au cel puțin una diferită de zero. Și toți minorii a căror ordine este mai mare de doi, sunt zero. Concluzie: gradul este 2. Sau, de exemplu, între minori de ordine zece au cel puțin un non-zero. Și toți minorii a căror ordine este mai mare de 10, sunt zero. Concluzie: gradul este de 10.

Desemnat rangul de matrice $ A $ ca: $ \ sunat A $ și $ r (A) $. Locul de zero matrice $ O $ presupus a fi zero, $ \ sunat O = $ 0 ° C. Să ne amintim că, pentru formarea matricei necesită rânduri expunged minore și coloane - dar pentru a șterge rânduri și coloane deasupra matricei în sine cuprinde imposibilă. De exemplu, dacă $ F $ matrice are o dimensiune 5 $ \ ori $ 4 alineatele (adică, conține 5 rânduri și 4 coloane), ordinea maximă a minorilor săi egal cu patru. Minorii forma a cincea comandă nu va avea succes, deoarece cele 5 coloane este necesară pentru ei (și avem un total de 4). Aceasta înseamnă că rangul matricei $ F $ nu poate fi mai mult de patru, și anume, $ \ $ F≤4 Rang.

Într-o formă mai generală de mai sus înseamnă că dacă matricea conține rânduri $ m $ și $ n $ coloane, atunci rangul său nu poate să depășească cea mai mică dintre numere $ m $ și $ n $, adică $ \ A≤ Rang \ min (m, n) $.

În principiu, definiția însăși de rang ar trebui să fie metoda locației sale. Procesul de găsire a matricei pentru a determina rangul poate fi reprezentată schematic după cum urmează:

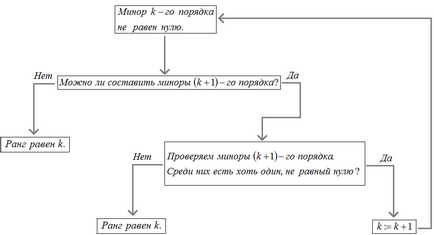
Voi explica acest circuit mai detaliat. Începem să vorbim încă de la început, adică, minori cu o matrice de ordinul I $ A $.

1. Dacă toți minorii de ordinul întâi (adică, elementele de matrice $ A $) sunt zero, atunci $ \ sunat A = 0 $. În cazul în care în rândul minorilor din ordinul întâi au cel puțin un non-zero, atunci $ \ sunat A≥ 1 $. Vom proceda la inspecția minorilor de ordinul al doilea.
2. În cazul în care toți sunt de ordinul a doua minori zero, atunci $ \ sunat A = 1 $. Dacă printre minori de ordinul al doilea au cel puțin un non-zero, atunci $ \ sunat A≥ $ sau 2. Vom proceda la inspecția celui de al treilea ordinul a minorilor.
3. În cazul în care toți minorii de ordin al treilea sunt zero, atunci $ \ A sunat = 2 $. În cazul în care în rândul minorilor de ordinul trei au cel puțin un non-zero, atunci $ \ sunat A≥ 3 $. Vom proceda la inspecția ordinii minorilor patra.
4. În cazul în care toți minorii din ordinul patra sunt zero, atunci $ \ A sunat = 3 $. În cazul în care în rândul minorilor ordinul al patrulea există cel puțin un non-zero, atunci $ \ sunat A≥ $, 4. Vom proceda la inspecția ordinii minorilor a cincea, și așa mai departe.

Ceea ce ne așteaptă la sfârșitul acestei proceduri? Este posibil ca printre minori ai ordinului k există cel puțin un non-zero, iar toți minorii (k + 1) th comanda va fi zero. Acest lucru înseamnă că k - ordinea maximă a minorilor, printre care există cel puțin un non zero, adică, Locul este egal cu k. Poate situația este diferită: în rândul minorilor de ordinul k va avea cel puțin un non-zero, iar minorii (k + 1) nu va fi în măsură să formeze de ordine. În acest caz, de asemenea, egal cu gradul k. Pe scurt, ordinea ultimului minor de zero compilat și va fi egală cu rangul matricei.

Ne întoarcem la exemplele în care procesul de identificare a matricei pentru a determina rangul vor fi ilustrate grafic. Încă o dată, subliniez că, în exemplele acestei teme vom găsi rangul de matrice, folosind o definiție a rang. Alte metode de calcul (matrice de rang minori metoda dantelate. Metoda de calcul matrice transformări elementare Rank) sunt luate în considerare următoarele subiecte.

Apropo, nu este necesar să se înceapă procedura de a găsi cea mai mică ordine minori rang, ca în exemplele de №1 și №2. Puteți merge direct la minorii de ordin superior (vezi. Exemplul №3).

Găsiți rangul de matrice $ A = \ stânga (\ începe 5 0 -3 0 2 \\ 7 0 -4 0 3 \\ 2 0 -1 0 1 \ end \ dreapta) $.

Această matrice are o dimensiune de \ $ de 3 ori 5 $, adică Acesta cuprinde trei rânduri și cinci coloane. Dintre numerele 3 și 5, minimul este de 3, prin urmare, gradul de $ A $ nu este mai mare de 3, adică $ \ A≤ Rang 3 $. Și această inegalitate este evident, deoarece minori patra formularul de comandă nu mai putem, - pentru ei ai nevoie de 4 linii, și avem doar 3. Ne întoarcem direct la procesul de a găsi un anumit grad de o matrice.

Dintre minori de ordinul întâi (adică printre elementele matricei A $ $) este nenul. De exemplu, 5, -3, 2, 7. In general, nu ne interesează în numărul total de elemente nenule. Există cel puțin un element de bază non-zero, - și asta e de ajuns. Deoarece printre minorii din ordinul întâi au cel puțin un non-zero, atunci putem concluziona că $ \ sunat A≥ $ 1 și du-te pentru a verifica minorii de ordinul al doilea.

Pentru a începe să investigheze a doua ordine minori. De exemplu, la intersecția liniilor №1, și coloane №1 nr.2, №4 sunt elemente minore astfel: $ \ left | \ începe 5 0 \\ 7 0 \ end \ dreapta | $. Acest determinant toate elementele din a doua coloană de la zero, și, prin urmare, factorul determinant în sine este egal cu zero, adică $ \ Stânga | \ începe 5 0 \\ 7 0 \ end \ dreapta | = 0 $ (vezi proprietatea №3 în proprietățile de subiect ale determinanților.). Alternativ, puteți calcula trivial acest determinant, folosind formula №1 a secțiunii privind calcularea factorilor determinanți ai doua și a treia comenzi.

$$ \ left | \ begin 5 0 \\ 7 0 \ end \ dreapta | = 5 \ cdot 0-0 \ cdot 7 = 0. $$

În primul rând am testat a doua minoră a fost egal cu zero. Ce înseamnă acest lucru? Faptul că necesitatea de a verifica în continuare minorii de ordinul al doilea. Fie toate acestea sunt zero (și apoi rangul este egal cu 1), oricare dintre ele există cel puțin un minor, non-zero. Să încercăm să pună în aplicare o alegere mai bună prin scrierea minoră a doua ordine, elementele care sunt situate la intersecția liniilor №1, №2 și coloane №1 și №5: $ \ left | \ începe 5 2 \\ 7 3 \ end \ dreapta | $. Noi găsim semnificația acestui al doilea ordin minor:

$$ \ left | \ begin 5 2 \\ 7 3 \ end \ dreapta | = 5 \ cdot 3-2 \ cdot 7 = 1. $$

Acest lucru minor nu zero. Concluzie: în rândul minorilor de ordinul al doilea au cel puțin una diferită de zero. De aceea, \ $ sunat A≥ $ sau 2. Este necesar să se procedeze la investigarea minorilor de ordin al treilea.

În cazul în care minorii pentru a forma a treia comanda vom selecta coloana sau coloana №2 №4, că astfel de minori vor fi zero (deoarece acestea vor conține coloana zero). Rămâne să verifice o singură comandă treime minoră, elementele care sunt situate la intersecția coloanei №1, №3, №5 și linii №1, №2, №3. Scriem acest minor și găsi sensul:

$$ \ left | \ begin 5 -3 2 \\ 7 -4 3 \\ 2 -1 1 \ end \ dreapta | = -20-18-14 + 16 + 21 + 15 = 0. $$

Deci, toți minorii din al treilea ordin sunt zero. Ultima compilate de către noi nenulă minoră a fost al doilea ordin. Concluzie: ordinea maximă a minorilor, printre care există cel puțin un non-zero este egal cu 2. Prin urmare, $ \ sunat A = 2 $.

Găsiți Locul de $ matrice A = \ stânga (\ începe -1 3 2 -3 \\ 4 -2 5 1 \\ -5 0 -4 0 \\ 9 7 8 -7 \ end \ dreapta) $.

Avem o matrice pătrată a patra ordine. Acum, observăm că gradul de această matrice nu este mai mare de 4, adică $ \ $ A≤ Rang, 4. Ne ajunge în jos pentru a găsi rangul unei matrice.

Dintre minorii din ordinul întâi (și anume, printre elementele matricei A $ $) are cel puțin o nenulă, deci $ \ sunat A≥ 1 $. Vom proceda la inspecția minorilor de ordinul al doilea. De exemplu, la intersecția liniilor №2, №3 și coloane №1 și №2 se obține un al doilea ordin minor: \ $ din stânga | \ Începe 4 \\ -2 -5 0 \ end \ dreapta | $. Să ne calcula:

Dintre minorii de ordinul al doilea au cel puțin un non-zero,, astfel încât $ \ sunat A≥ $ sau 2.

Să trecem la minori de ordinul trei. Am găsi, de exemplu, elemente minore, care sunt situate la intersecția rândurilor №1, №3, №4 și coloane №1, №2, №4:

$$ \ left | \ Begin -1 3 \\ -3 -5 0 0 \\ 9 7 -7 \ end \ dreapta | = 105-105 = 0. $$

Deoarece ordinul a treia minoră a fost egal cu zero, atunci ai nevoie pentru a investiga un ordin al treilea minor. Fie că sunt egale cu zero (atunci gradul este egal cu 2), oricare dintre ele există cel puțin un non-zero, (apoi să ne exploreze minorii de un sfert de ordinul). Luați în considerare ordinea treilea minor, elementele care sunt situate la intersecția rândurilor №2, №3, №4 și coloane №2, №3, №4:

$$ \ left | \ Inceput -2 5 1 \\ 0 -4 0 \\ 7 8 -7 \ end \ dreapta | = -28. $$

Dintre minorii de ordinul a treia au cel puțin un non-zero,, astfel încât $ \ sunat A≥ 3 $. Vom proceda la inspecția ordinii minorilor patra.

Orice comandă minoră a patra este situat la intersecția a patru linii și patru coloane $ A $. Cu alte cuvinte, minore, pentru a patra - aceasta este determinantul matricei $ A $, din moment ce aceasta este doar o matrice care cuprinde 4 rânduri și 4 coloane. Determinantul acestei matrice a fost calculată în temă Exemplul №2 „Coborârea determinantului ordine. Expansiunea determinantului de-a lungul unui rând (coloană)“. astfel încât să ia doar rezultatul final:

$$ \ left | \ Begin -1 3 2 -3 \\ 4 -2 5 1 \\ -5 0 -4 0 \\ 9 7 8 -7 \ end \ dreapta | = 86. $$

a patra comandă Deci minor nu este zero. Minorii formularul de comandă a cincea nu putem. Concluzie: cel mai înalt ordin al minorilor, printre care există cel puțin un non-zero este egal cu 4. Rezultatul: $ \ sunat A = 4 $.

Găsiți Locul de $ matrice A = \ stânga (\ începe -1 0 2 -3 \\ 4 -2 5 1 \\ 7 -4 0 -5 \ end \ dreapta) $.

Acum observăm că această matrice conține 3 rânduri și 4 coloane, astfel încât $ \ $ 3 A≤ sunat. În exemplele anterioare, vom începe procesul de găsire a unei clasări considerare minori cea mai scăzută (prima) ordine. Aici vom încerca să verifice imediat minorii cea mai bună ordine posibilă. Pentru matricea $ A $ astfel minori sunt triplu. Luați în considerare elementele minore de ordinul al treilea se află la intersecția liniilor №1, №2, №3 și coloane nr.2, №3, №4:

$$ \ left | \ Începe 0 2 -3 -2 \\ 5 1 \\ -4 0 -5 \ end \ dreapta | = -8-60-20 = -88. $$

Astfel, cel mai înalt ordin al minorilor, printre care există cel puțin un nenulă, egal cu 3. Prin urmare, rangul matricei este 3, adică, $ \ A = 3 Rang $.

În general, găsirea rangul matricei pentru a determina - în cazul general, problema este destul de consumatoare de timp. De exemplu, matricea este relativ mică de 5 $ \ ori4 $ 60 este prevăzută cu un al doilea ordin minori. Și chiar dacă 59 dintre ele sunt egale cu zero, minorul 60 poate fi non-zero. Apoi, va trebui să exploreze minorii de al treilea ordin, care, în această matrice de 40 de bucăți. De obicei, ei încearcă să utilizeze o metode mai puțin greoaie, cum ar fi o metodă de minori dantelate sau metode transformări echivalente.