Distribuția normală în Excel
Evaluare: 5/5
legea normală - baza și consecință a mai multor metode statistice. Dar nu din cauza faptului că datele originale sunt distribuite în mod normal, nu este așa, ci pentru că există un motiv mai puternic - teorema limitei centrale. Prin urmare, legea normală este folosit mult mai frecvent decât apare în natură.
Matematic legea normală este o funcție cu care probabilitatea de a găsi o variabilă de la valorile date. Acesta poate fi, și vice-versa, se calculează valoarea variabilei pe aceste probabilități. Acest lucru va necesita o funcție inversă a distribuției normale. În minte, în conturi, sau chiar un calculator pentru a efectua astfel de calcule foarte problematice, astfel încât există mese speciale. Apropo, cea mai bună colecție de tabele statistice sunt în bibliotechke.
Utilizați tabelele în sine sa dovedit a fi bine, dar există o modalitate mai eficientă de a calcula probabilitatea. Acest Excel, care oferă funcții speciale pentru prelucrarea datelor distribuite în mod normal. Există mai multe dintre ele.
După cum se știe, distribuția normală N (p, σ 2) depinde de doi parametri: așteptare (μ) și o variație (σ 2). O distribuție normală standard, ele sunt, respectiv, 0 și 1, adică, N (0, 1). A fost creat pentru tabelul de date normalizat menționat mai sus.
Apoi, ne vom concentra asupra funcțiilor Excel (denumite formule, nu trebuie confundat cu funcții de distribuție), puteți utiliza pentru a automatiza (adică o mie de ori pentru a accelera) procesul de găsire a probabilităților.
funcţia NORM.ST.RASP
NORM.ST.RASP formulă este utilizată pentru a calcula densitatea φ (z) sau probabilitatea φ (z) a datelor normalizate (z). Sintaxa formulei următoare.
z - valoarea standardizată a variabilei
Integral - dacă 0 φ densitate calculată (z). dacă 1 - valoarea funcției F (z), adică, probabilitatea P (Z Traducerea în limba română a ultimului câmp, desigur, a pus în lumină. Și se calculează valoarea funcției densității pentru orice z: -3, -2, -1, 0, 1, 2, 3 (care menționăm în celula A2). Pentru a calcula necesară densitate = formula NORM.ST.RASP (A2; 0). Graficul de mai jos - acesta este un punct roșu. Pentru a calcula valorile NORM.ST.RASP = (A2; 1). Pe diagrama - zona umbrită de sub curba normală. În realitate, de multe ori trebuie să conta probabilitatea ca o valoare aleatorie nu va depăși anumite limite din media (în deviația standard corespunzătoare variabilei z), adică, P (| Z | Definirea, ceea ce este probabilitatea unei variabile aleatoare care se încadrează în ± 1Z, ± 2Z și 3Z ± zero. Pentru aceasta este necesar să se utilizeze una dintre caracteristicile oricărei distribuții continue și să ia diferența: F (z) -F (-z), sau care dau același rezultat, 2F (z) -1. În Excel va arăta după cum urmează: = 2 * NORM.ST.RASP (A2; 1) -1. Diagrama în mod clar proprietățile de bază vizibile ale distribuției normale, inclusiv trei regula sigma. conform căreia ± 3 abateri standard de la valorile medii aproape toate închise. Acesta poate fi problema inversă: de probabilitatea P existent (Z Formula NORM.ST.OBR calculeaza inversul distribuției normale standard. Sintaxa constă dintr-un singur parametru: probabilitate - probabilitatea. Această formulă poate fi utilizată la fel de des ca și cea anterioară, pentru că în aceleași tabele trebuie să se uite nu numai probabil, dar cuantila (cele z, ce corespunde unei probabilități). Atribuirea efectivă a sarcinilor diferă în mod tipic și trebuie să utilizeze orice design folosind această formulă. Este necesar să se amintească intervalele de încredere. care depind de nivelul de încredere. Aceasta este abaterea de la medie, numai de data aceasta probabilitatea specificată, iar valoarea calculată z.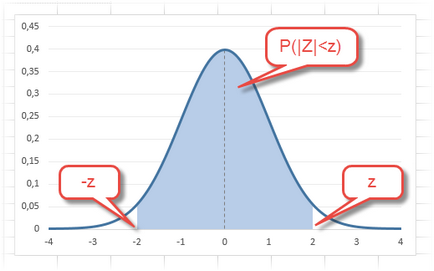
funcţia NORM.ST.OBR
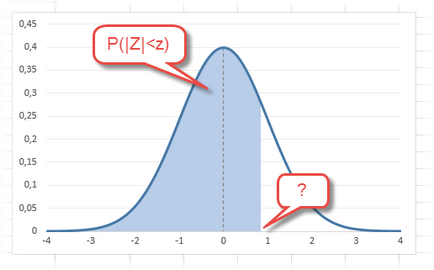
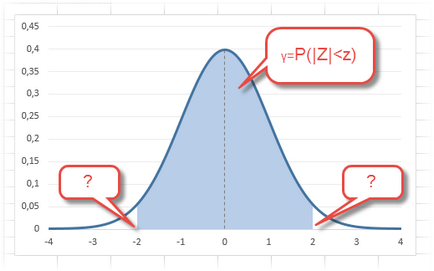
Dat fiind că intervalul de încredere este compus din limitele superioare și inferioare, precum și că distribuția normală este simetrică în raport cu zero, este suficient să se calculeze limita superioară (deviație pozitivă). Limita inferioară este luată cu semn negativ. Notăm probabilitatea de încredere ca γ (gamma), apoi toleranța se calculează cu următoarea formulă
Acum, se calculează valorile z (care corespunde cu abaterea de la medie într-un Sigma) pentru mai multe probabilități, inclusiv cele care sunt cunosc pe de rost toate statisticile, și anume intervale de încredere pentru probabilitatea de 90%, 95% și 99%. In celula B2 menționăm formula: NORM.ST.OBR = ((1 + A2) / 2). Prin variația valorii variabilei (probabilitate în celula A2) obținem diferite intervale limită.
Ca interval de încredere văzut de 95% este 1.96, care este de aproape două abateri standard. Prin urmare, posibila răspândire a variabilei aleatoare normale, mai degrabă cu ușurință chiar și în estimarea minte (de exemplu, media aritmetică, care, în virtutea teoremei limită centrală are o distribuție normală). În general, un nivel de încredere de 90%, 95% și intervale de încredere de 99% corespund ± 1,64, ± 1,96 și ± 2,58 σ.
NORM.ST.RASP și NORM.ST.OBR funcții generale permit de a face orice calcule asociate cu o distribuție normală. Dar, în scopul de a facilita și de a reduce numărul de acțiuni în Excel, există alte câteva caracteristici. De exemplu, pentru calcularea intervalelor de încredere ale mediei pot fi utilizate DOVERIT.NORM. Pentru a testa ipoteza statistică cu privire la media aritmetică este formula Z.TEST. Dar, din nou, puteți face fără ele dacă utilizați structura formulelor de mai sus.
Luați în considerare câteva exemple de formule utile.
funcţia NORM.RASP
Funcția NORM.RASP diferă de NORM.ST.RASP numai prin faptul că acesta este utilizat pentru a procesa datele de orice dimensiune, nu doar standardizate. parametrii normali de distribuție sunt specificate în sintaxa.
media - speranța de a fi utilizat ca primul parametru al modelului de distribuție normală
standard_dev - abaterea standard - al doilea parametru de model
Integral - dacă este 0, atunci densitatea este calculată, dacă este 1 - valoarea funcției, adică, P (X De exemplu, pentru a calcula valoarea densității pentru 15 este îndepărtată din probă normală cu o așteptare matematică 10, o deviație standard de 3 pentru a scrie următoarea formulă: În cazul în care ultima opțiune este de a pune 1, atunci obținem probabilitatea ca o variabilă aleatoare normală va fi mai mică de 15 pentru parametrii date de distribuție. Astfel, probabilitatea poate fi calculată direct din datele inițiale. Aceasta este funcția inversă a distribuției normale. Sintaxa este după cum urmează. probabilitate - probabilitatea standard_dev - abaterea standard Definițiile sunt la fel, nu se va repeta. Atribuirea la fel ca și cea a NORM.ST.OBR, numai această funcție operează cu date de orice dimensiune, care, desigur, în formula indică parametrii legii normale. Un exemplu este prezentat în video la sfârșitul anului. Funcțiile descrise mai sus, facilitează foarte mult viața și de a salva timp. Dar cel puțin poți face fără ele, pentru că există tabele statistice. Dar, uneori, fără formule în nici un fel. Un exemplu este generarea de numere aleatoare. În Excel, există două caracteristici care dau numere aleatoare. Prima dintre acestea RANDBETWEEN. Acesta furnizează un numere întregi aleatoare uniform distribuite în limitele specificate. Puteți, de exemplu, selectați în mod aleatoriu câștigătorii unui concurs sau a crea o parolă. A doua funcție a RAND generează un număr aleator uniform distribuit între 0 și 1. Este este necesară această funcție pentru a face un eșantion artificial cu o anumită distribuție (nu doar normal). RAND va genera o probabilitate aleatoare, care au și limite de la 0 la 1. O descriere folosind o funcție inversă a unei distribuții normale (standard sau convenționale) care sunt convertite în numere normale. Să presupunem pentru experimentul trebuie să obțină un eșantion de distribuit în mod normal, cu speranța matematică din populația totală de 10 și o deviație standard de 3. Pentru o singură valoare aleatoare a scrie formula Trageți-l la numărul de celule dorit, iar proba normală este gata. Pentru a simula datele standardizate ar trebui să fie utilizate NORM.ST.OBR. Procesul de conversie este uniformă în număr normale poate descrie vizual prin graficul de mai jos. Din probabilitatea uniformă, care sunt generate de formula RAND, trage o linie orizontală la graficul funcției normale de distribuție. Apoi, probabilitățile punctelor de intersecție cu graficul omisa proiecție pe axa orizontală.funcţia NORM.OBR
Generatorul normal de numere aleatorii
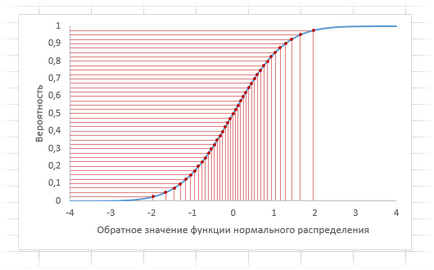
La valorile de ieșire obținute cu o concentrație tipică în apropierea centrului. E o întoarcere a alerga prin funcția de distribuție normală a numărului de spire în uniforma normală. Excel vă permite să joace orice număr de probe de orice dimensiune în câteva secunde.
Ca de obicei, video de însoțire, în cazul în care toate cele de mai sus este prezentată în acțiune.