Greutatea sistemului

mișcarea sistemului, în plus față de forțele de operare, este de asemenea dependentă de masa sa totală și distribuția masei. masa sistemului este egală cu suma aritmetică a maselor tuturor punctelor sau organismelor care constituie sistemul

Într-un câmp gravitațional uniform, pentru asta. greutate corporală în fiecare particulă va fi proporțională cu greutatea sa. Prin urmare, pe distribuția masei în organism poate fi judecat de poziția centrului de greutate. Transformata formule centrul de greutate coordonate care determină:

Ecuațiile rezultate sunt doar masa puncte materiale (particule) care formează corpul și coordonatele acestor puncte. În consecință, poziția punctului C (xC. YC. ZC) într-adevăr caracterizat distribuția zată-masa în organism sau în orice B-tem mecanic dacă sub. înțeleasă în mod corespunzător masei și coordonatele punctelor sistemului.

C. Punctul geometric al cărui coordonate sunt determinate prin formula menționată, denumit în centrul de masă sau a centrului de masă al sistemului.

Centrul de greutate este determinată de vectorul de raza

unde - vectorii de poziție ale punctelor sistemului de formare.

Deși poziția centrului de masă coincide cu centrul de greutate situat într-un câmp gravitațional uniform, aceste concepte nu sunt identice. Conceptul centrului de greutate ca un punct prin care linia de acțiune a forțelor rezultante ale gravitației, în esență, face sens doar pentru un solid, găsindu-schegosya într-un câmp gravitațional uniform. Conceptul se referă la centrul de masă ca o caracteristici de distribuție în masă ale sistemului, are sens pentru orice sistem de puncte materiale sau organisme, în cazul în care acest concept își păstrează semnificația sa, indiferent dacă această tulpină B sub influența a ceea ce unele forțe sau nu.

Momentul de inerție în jurul axei. Raza de inerție-TION.

Centrul de greutate caracterizează distribuția masei a sistemului nu este plin. De exemplu (Fig.32), în cazul în care distanța h de axa Oz fiecare dintre sfere identice A și creștere B cu aceeași sumă, poziția centrului de sistem de masă nu se schimbă, iar distribuția masei devine diferită, iar acest lucru va afecta mișcarea sistemului (rotație în jurul axei Oz ceteris paribus va fi mai lentă).

Prin urmare, mecanica introdusă o altă caracteristică a distribuției de fisiune în masă - momentul de inerție. Inertsiitela de cuplu (sistem) în raport cu această axă Oz (sau un moment de inerție axial) este un scalar egal cu suma produselor maselor de toate punctele corpului (sistem) în pătrate de distanțele față de această axă

Din definiția rezultă că momentul de inerție (sau sisteme) în raport cu orice axă este o valoare pozitivă nu este egal cu zero.

Rețineți, de asemenea, că momentul de inerție - este caracteristicile geometrice ale corpului, care este independent de mișcarea sa.

Momentul de inerție axial joacă un rol similar în timpul mișcării de rotație a corpului, care masa în translație, adică care este momentul de inerție axial UI corp roi inerție atunci când Vera-atenție mișcarea.

În conformitate cu formula moment de inerție egală cu suma momentelor de inerție-ing toate părțile sale, în raport cu aceeași axă. Pentru ML-clorhidric punct material locat-dyascheysya la o distanță h față de axa.

De multe ori în cursul calculelor utilizează conceptul de raza de girație. Corp raza de inerție în jurul axei Oz este o valoare liniară. definită de ecuația

unde M - masa corpului. Din definiția rezultă că raza de girație este distanța de la axa geometrică Oz punctul în care este necesar să se concentreze întreaga greutate corporală la momentul de inerție al acestui punct unic este egal cu momentul de inerție al corpului.

În cazul celor solide la, de rupere-l în părți elementare, constatăm că, în limita sumei pe egalitatea, la rândul său, integrală. Ca urmare, ținând cont de ceea ce-. unde - densitatea și obținem volumul V

Integrala este peste volumul întregului V al corpului, iar densitatea și distanța h depind de coordonatele punctelor corpului.

Momentele de inerție ale unor corpuri omogene:

1.Tonky tijă omogenă de lungime l și masa M. calcula momentul său de inerție în raport Az-telno axa perpendiculară pe tija și proho-dyaschey prin capătul său A (fig. 33).

Regizat de-a lungul AB axe de coordonate Ax. Apoi, pentru fiecare segment elementar din valoarea dx lungime h = x și masa, unde - lungimea unei unități de masă a tijei. Ca rezultat,

Înlocuirea valorii sale, în cele din urmă vom obține:

2. uniform subțire circular raza inelului R și masa M. Descoperim momentul său de inerție față de axa Cz perpendiculară pe planul inelului și care trece prin centrul (Fig.34 a). Deoarece toate punctele de pe inelele sunt în regiunea Cz axa hk = R, atunci

În consecință, pentru inelul

Evident, același rezultat se obține pentru timpul subțire de masă cilindrică cochilie M și raza R inerție, dar în raport cu axa sa.

3. Runda omogen placa sau raza cilindrului ra-R și calcula momentul de inerție în masă M. pla Stina axa circulară relativ Cz perpendicular pe placa si proho-dyaschey prin centrul său (a se vedea. Fig.34, a). Pentru a face acest lucru vom selecta inelul elementar de rază r și dr lățime (Fig.34, b).

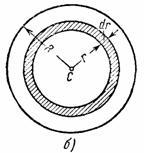
Dimensiunea acestui inel este, iar masa, unde - greutatea pe unitatea de suprafață a plăcii. Apoi, pentru inelele elementare selectate vor

în timp ce pentru întreaga placă. Înlocuirea valorii sale, în cele din urmă am

Aceeași formulă va fi, evident, pentru momentul de inerție al unui cilindru circular de masă uniformă M și raza R în jurul axei sale Oz (ric.34, c).

4. O placă dreptunghiulară, con, bilă. Omiterea calculele, vom prezenta formulele care definesc momentele de inerție următoarele organisme:

. A) placă dreptunghiulară continuă a masei M cu laturile a și AB = BD = b (axa x de-a lungul partea AB axa y - de-a lungul BD):

b) continuă con circular drept cu masa M cu o rază R de bază (axa z este direcționată de-a lungul axei conului)

d) o masă M solid și raza R bilă (axa z este direcționat de-a lungul unui diametru)