Indoire Analiza grinzilor static nedeterminate
8.10.1. cu o singura grinda
Sunt fascicul static nedeterminat, în care toate reacțiile nu pot fi determinate din ecuațiile staticii singur. Astfel, grinda din Fig. 8,44, și are trei reacții necunoscute. . și statice și numai două ecuații și. Iar pentru fasciculul din Fig. 8.44, b patru reacții necunoscute:. . și. Numărul de ecuații staticii, la fel ca în cazul precedent, aceleași două condiții sunt egale cu zero toate momentele în ceea ce privește legarea de referință.
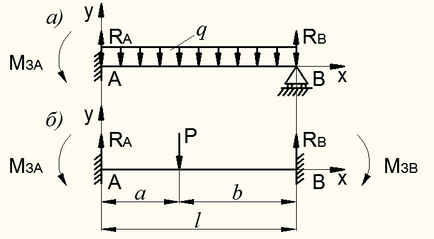
Figura 8.44 - de nedeterminat static, _balki cu un singur interval
Diferența în numărul răspunsurilor și numărul de ecuații statice numit gradul de redundanță a fasciculului.
Pentru grinzi ris.8.44, iar gradul de redundanță este. a spus că, odată ce fasciculul este incertă static. Pentru grinzi ris.8.44 b. și anume fascicul nedeterminat de două ori static. Astfel, grinzile sunt nedeterminate static așa-numitele „extra“ necunoscute în raport cu numărul de ecuații staticii. Pentru a le determina folosind starea de compatibilitate de deformare, elaborarea, care ia în considerare următoarele exemple:
Exemplul 9.9.1. Dezvăluirea redundanță și calculul fasciculului de îndoire (ris.8.45 asemenea).
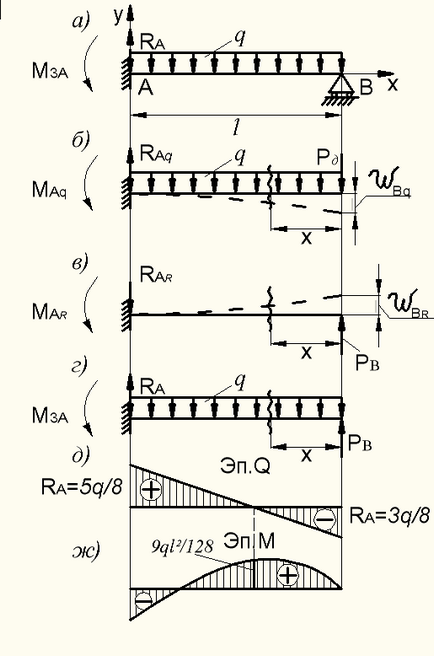
unde - devierea fasciculului de q sarcină pentru îndepărtarea suportul mental B (a se vedea figura 8.45, b ..); - devierea fasciculului de forța (reacție) (a se vedea figura 8.45 în ..).
Noi calcula devierile pe baza Mora integrale.
T mnQZnU8x9mMIP7jiCJJXAwUPAjXS4dQr2fgi / OfDsNSz9lIXQXZMqkHGjJU + 0OiZGzh0fd6Hvk2P 7cmh2CGxBoYpx61EoQbzhZIOJzyj9vOGGUGJeq2xOfPxZOJXIiiT6VmCijm15KcWpjlCZdRRMogr F9bI563hEptYysCv7 / aQySFnnNxA + 2HL / Gqc6sHrz79g + RsAAP // AwBQSwMEFAAGAAgAAAAhAIHn VGPgAAAACwEAAA8AAABkcnMvZG93bnJldi54bWxMj8FOg0AQhu8mvsNmTLzRBYKtRZbGaOzNGNFU jws7ApGdJey2xT59x5MeZ + bLP99fbGY7iANOvnekIFnEIJAaZ3pqFby / PUW3IHzQZPTgCBX8oIdN eXlR6Ny4I73ioQqt4BDyuVbQhTDmUvqmQ6v9wo1IfPtyk9WBx6mVZtJHDreDTON4Ka3uiT90esSH Dpvvam8V + CZe7l6yavdRyy2e1sY8fm6flbq + mu / vQAScwx8Mv / qsDiU71W5PxotBQZQlN + weFGTp CgQTUbLmRc3oKk5BloX836E8AwAA // 8DAFBLAQItABQABgAIAAAAIQC2gziS / gAAAOEBAAATAAAA AAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If / WAAAA lAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAOGhBudDAgAA UwQAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAIHnVGPg AAAACwEAAA8AAAAAAAAAAAAAAAAAnQQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAACq BQAAAAA = "strokecolor =" white [3212] „>
Figura 9.45 - Calculul fasciculului nedeterminat static
. La determinarea deviației la t B q sarcină distribuită introduce mental rezistență suplimentară (a se vedea figura 8.45, b ..):
Devierea capătului puterii consolei este egală cu (a se vedea figura 8.45 în ..):
Bazat pe condițiile (8.63), echivalând expresiile (8.64) și (8.65) pentru devierea fasciculului în t In .:
Găsirea. Obținem fascicul static determinate, încărcate transversal intensitate distribuită q sarcină și are o anumită forță (reacție) (Fig. 8.45 g). Pentru a construi această grindă diagramă și M (fig. 8.45 d. W). numărare x coordonata capătul din dreapta al fasciculului m. In.
amâne coordonatele obținute de pe ep. și conectați-le printr-o linie dreaptă - o relație liniară ep. (A se vedea. Fig. 8.45, d).
După cum se poate observa din expresia. îndoire Diagrama momentului corespunde unei parabole pătratice în ceea ce privește coordonatele x. Doi dintre ei ordonatei în Tovarăși A. Așa cum este definit deja. Pentru a găsi ordonata ep. M într-o secțiune unde. efectua calcule suplimentare.
Din condiția obținem extreme ale unei funcții M:
Grinzile secționale au o extremum a funcției la M în intervalul grinzii:
Rezultat a disponibiliza pe ep ordonata. Când M (vezi. Fig. 8.45 g).
Exemplul 9.9.2. Pentru fasciculul care este fixat de ambele capete (fig. 8.46, a) și este îndoit de o forță concentrată R. relevă incertitudinea statică și de a construi și diagrame.
După cum sa menționat mai sus, considerată fascicul de două ori nedeterminat static: reacții necunoscute - patru. și condiții statice - două.
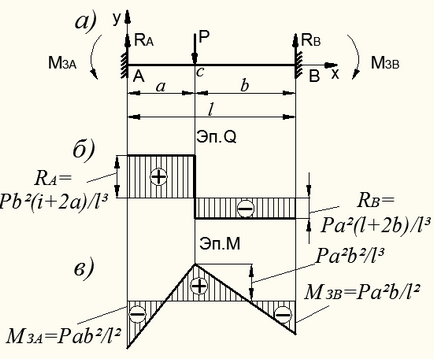
Figura 8.46 - Calculul fasciculului nedeterminat static
Din condiții statice, avem:
Dat fiind faptul că unghiul de rotație și deformare a secțiunii de susținere B sunt egale cu zero, obținem două ecuații pentru determinarea reacțiilor lipsă - condiții de compatibilitate sușa:
Rezolvarea ecuațiilor obținute (8.67) și (8.68) găsim reacția:
Acum este ușor de a construi diagrame de forțe de forfecare și a momentelor de încovoiere. În acest scop, vom calcula momentul de încovoiere la secțiunea C, în conformitate cu forța F:
Diagrame și prezentate în Fig. 8.46, b. în.
8.10.2. Un fascicul multi-deschiderea continua
A grinzi continue, multi-numita având mai mult de un zbor. Ele sunt nedeterminat și divulgarea static lor de concediere este convenabil pentru a efectua metoda de ecuații cu trei momentului. Un exemplu foarte simplu, ia în considerare esența acestei metode.
Exemplul 9.3. Pentru grinda (fig. 8.47, a) cu excepția lagărelor culbutori la capete are un suport intermediar. Necunoscutele în calculul acestor grinzi de îndoire sunt trei reacții asupra suporturilor și condiții statice - două. Prin urmare, această fază va fi o dată nedeterminată static.
Divulgarea redundanță teorema a trei puncte pentru necunoscut în plus primește puncte de referință M pe suportul intermediar 2. tăiere mintea ei și împărțind fasciculul în două singură deschidere (ris.8.47 b), aceste momente sunt determinate de condițiile de compatibilitate a tulpinilor:
unde - unghiul de rotație al dreptului secțiunii 2 a grinzii unice între suporturile 1 și 2 de sprijin;
- unghiul de rotație al stânga susținere secțiunea 2 a grinzii unice între suporturile 2 și 3.
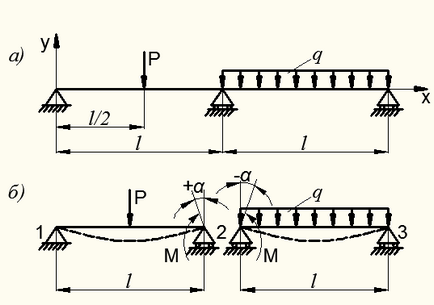
Figura 8.47 - Calculul grinzii doua deschideri, prin Teorema trei _momentov
Aceste unghiuri de rotație pe baza regulilor de semne (.. A se vedea figura 8.47, b) sunt exprimate prin intermediul punctelor de încărcare și de referință externă:
Pe baza expresiilor (8.72) și (8.73) cu (8.71) obținem o ecuație pentru determinarea necunoscut redundant M:
După găsirea unui zbor suplimentar necunoscut fiecare fascicul este privit ca un grinzi încărcate cu excepția determinate static sarcina externă are un anumit momente de referință.
dezvăluire Metoda nedeterminare statică mai multor deschideri, grinzi teorema de trei momente numite astfel deoarece, atunci când un număr arbitrar de treceri fasciculului în fiecare ecuație deformațiilor unghiulare de compatibilitate tip (8,74) nu va include mai mult de trei puncte de sprijin pentru examinare -lea suport intermediar sub tipul condiției (8.71).
Calculul elementelor de îndoire fiecare interval după determinarea necunoscutelor redundante ca fascicul static determinate este produsă prin amestecarea (însumarea) a elementului de îndoire din sarcina externă și punctele de referință tranzitul este deja definit. Astfel, în acest exemplu, care rezultă îndoire Diagrama momentului pentru fiecare deschidere a fasciculului. obținut prin suprapunând ep. de la o sarcină predeterminată pe un ep de zbor. punctelor de referință
Pentru exemplul de mai sus este prezentat umbrit în Fig. 8.48:
Pentru primul zbor. pentru al doilea pasaj. Astfel, reacția superpoziție determinat pe suporți și ep este construit. .
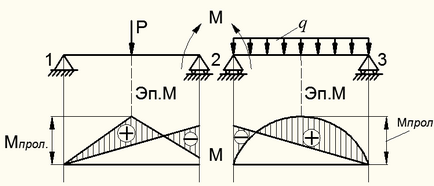
Figura 8.48 - Construirea unei metode de acoperire moment de încovoiere