Limita Minunat - l

Luați în considerare limitele pe o față și, și să dovedească că acestea sunt egale cu 1.

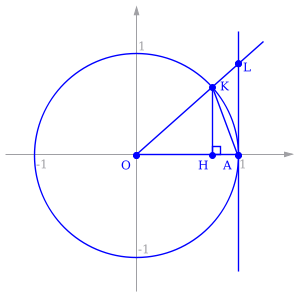
Să. Amână acest unghi pe cercul unitate (R = 1).

K Point - punctul de intersecție al fasciculului cu un cerc, iar punctul L - cu tangenta la cercul unitate la un punct (1, 0). puncte de proiecție K pe axa OX - Punct H.

Substituind în (1), obținem:

Înmulțit cu sinx:

Să trecem la limita:

Găsiți o limită din stânga-verso:

și există limite față dreapta și stânga 1, și, prin urmare, limita este 1 în sine.

O a doua limită remarcabilă

Dovada a doua limită remarcabilă:

a doua limită remarcabilă Dovada pentru cazul secvenței (adică valori pozitive pentru x)

Demonstrăm mai întâi teorema pentru secvența

Din această ecuație (1) rezultă că odată cu creșterea în număr de n termeni pozitivi în creșterile în partea dreaptă. Mai mult, prin creșterea numărului n ubyvet, crescând astfel magnitudine. Prin urmare, secvența - este în creștere. în timp ce

Arătăm că este limitată. Înlocuiți fiecare suport de pe partea dreaptă de către unul, partea dreapta va crește, obținem inegalitatea

Consolidarea inegalitatea rezultată, înlocuiți 3,4,5, ... stând la numitorul numărului fracției 2:

Suma în paranteze găsi suma formula exponențial membri:

Astfel, secvența este mărginită de mai sus, în care următoarele inegalități (2) și (3).

Prin urmare, bazat pe teorema lui Weierstrass (secvența criteriu de convergență), secvența este în creștere și mijloace monoton limita restricțiilor este reprezentat de litera e. Ie

Știind că a doua limita remarcabila pentru adevaratele valori x pozitive, se dovedesc a doua limită remarcabilă pentru x reală, adică Demonstrăm că. Considerăm două cazuri:

1. Fie. Fiecare valoare a lui x se află între două numere întregi, unde n = [x] - este partea întreagă a lui x.

Rezultă că, așa. În cazul în care, atunci. Prin urmare, în conformitate cu limita, avem. Pe baza (o funcție a limitei intermediare) existența limitelor.

2. Să. Facem schimbarea - x = t. atunci

Din aceste două cazuri implică faptul că pentru orice x.

Consecințele a doua limită remarcabilă:

Limita logaritmică remarcabilă

limită indicativă remarcabilă

Limita de putere remarcabila

remarcabil nu este limita.
O limită bună - limita morții.

Vezi ce „limită minunat“ în alte dicționare:

e (număr) - Acest termen, există alte utilizări, vezi E. A nu se confunda cu numărul de tip Euler I .. A nu se confunda cu constanta lui Euler. Numerele irationale γ ζ (3) √2 √3 √5 φ α e π δ ... Wikipedia

Dezvăluirea de incertitudine - metode de prezentare a informațiilor de incertitudine pentru calcularea limitelor de funcții definite prin formulele care au ca rezultat substituirea formală în aceste valori extreme ale argumentului sunt lipsite de sens, care se transformă în expresii cum ar fi: ... ... Wikipedia

Limitele de incertitudine - Metode de incertitudine Dezvăluirea calculării limitelor funcțiilor formule definite care au ca rezultat substituție în aceste valori limită de argument formale sunt lipsite de sens, adică transformați în tipul de expresie. 0/0, 00 ... Wikipedia

Incertitudinea (matematică) - metode de incertitudine Dezvăluirea calculării limitelor funcțiilor formule definite care au ca rezultat substituție în aceste valori limită de argument formale sunt lipsite de sens, adică transformați în tipul de expresie. 0/0, 00 ... Wikipedia

incertitudini Dezvăluirea - metode de incertitudine Dezvăluirea calculării limitelor funcțiilor formule definite care au ca rezultat substituție în aceste valori limită de argument formale sunt lipsite de sens, adică transformați în tipul de expresie. 0/0, 00 ... Wikipedia

E (constantă matematică) - e constantă matematică, baza logaritmului natural și număr irațional transcendental. Uneori, numărul e numit numărul lui Euler (a nu se confunda cu m. N. Am facut un fel de numere ale lui Euler) sau numărul Napier. Notate cu litere mici «e». ... ... Wikipedia

Numărul Neperovo - e constantă matematică, baza logaritmului natural, număr irațional și transcendental. Uneori, numărul e numit numărul lui Euler (a nu se confunda cu m. N. Am facut un fel de numere ale lui Euler) sau numărul Napier. Notate cu litere mici «e». ... ... Wikipedia

anterior ◈ următoarea