Metoda curenților de buclă - studopediya

Metoda de curenții de buclă este una dintre principalele metode de calcul al circuitelor electrice complexe, care sunt utilizate pe scară largă în practică.

Când curenții de buclă prin calcularea cred că în fiecare circuit independent curge un curent de buclă. Ecuațiile sunt relativ curenții de buclă, după care ramurile curenții prin conturul curent.

Astfel, analiza a ochiurilor poate fi definită ca o metodă de calcul, în care, pentru a primi curenții de contur dorite. Numărul de necunoscute în această metodă este numărul de ecuații care ar trebui să facă pentru schema de legea lui Kirchhoff II, și anume, . Prin urmare, această metodă este mai economic în calcule decât metoda ecuațiile Kirchhoff.

Un algoritm de calcul al curenților de buclă de circuite pe exemplu circuit cu trei circuite independente (vezi Fig. 2.3). Să presupunem că fiecare circuit ia un curent în direcția indicată. Pentru fiecare dintre buclele formează ecuația legii lui Kirchhoff II. În acest caz, vom lua în considerare faptul că ramura adiacentă pentru curenții de buclă și (rezistor ramură bd. Include) fluxurile de curent. pe ramura adiacentă pentru curenții de buclă și (dc ramură. care cuprinde rezistor) curge curent

. pe ramura adiacentă pentru curenții de buclă și (ramura AD. care cuprinde rezistor) curge curent.

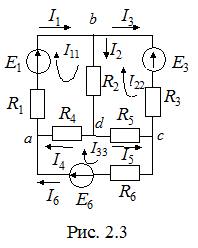
Apoi, în conformitate cu ecuațiile II legii lui Kirchhoff pentru fiecare circuit trebuie să ia forma următoare:

Noi grup termenii cu aceleași nume curenții:

circuite de rezistență proprii

;

circuite de rezistență comună

;

.

În forma sa finală a sistemului de ecuații pentru curentul buclei ia forma:

în formă de matrice

rezistență buclă adecvată (Rii) este suma aritmetică a rezistențelor tuturor consumatorilor din bucla i-lea.

Rezistența totală a circuitului (Rij = RJI) reprezintă suma algebrică a rezistențelor de ramură de consum (mai multe sucursale), ambele aparținând i -lea și j -lea contururi. Această sumă include rezistența cu semnul „+“ în cazul în care curenții de contur curg prin această rezistență într-o singură direcție (conform), iar semnul „-“ atunci când contra-flux.

Conturat EMF reprezintă suma algebrică a surselor EMF incluse în circuit. Cu semnul „+“, această sumă include sursele EMF, acționând în conformitate cu circuitul de by-pass, cu semnul „-“ EMF surse includ opuse care acționează.

Soluția sistemului rezultat este convenabil să se efectueze metoda de Kramer:

în care D, D1. D2. D3. - respectiv determinanților matrici:

,

Pentru rezultate prin curenții de contur I din legea Kirchhoff curente ramuri sunt determinate.

Astfel, DC curenții de buclă în buclă de calcul algoritm prin următoarele:

1. Identificarea tuturor curenții ramurilor și direcția pozitivă.

2. alege Arbitrar un set de p circuite independente, aplicate pe direcția pozitivă a diagramei de contur a curenților din circuit selectat.

3. Determinați propria comună de rezistență și de contur și să le înlocuiască EMF în sistemul de ecuații (2.6).

4. Lăsați sistemul rezultat al curenților de ecuații cu buclă, folosind regula lui Cramer.

5. Se determină curenții de ramură în ceea ce privește curenții de contur ale legii I Kirchhoff.

6. Dacă este necesar, folosind legea lui Ohm generalizată pentru a determina potențialele nodurilor.

7. Verificați balanța puterii.

Dacă q este conținută într-un lanț de surse de curent, cantitatea de ecuații co-așteptare este redus cu q și p este egal cu - q. deoarece curenții din aceste ramuri sunt cunoscute (pentru circuite cu ecuația Iii = J nu poate înregistra). În acest caz, ar trebui să alegeți un set de curenți în buclă independente pentru unele dintre ele au devenit celebru. Acest lucru presupune că fiecare sursă de curent este inclus doar într-un singur circuit. surse de tensiune UJ intră ca necunoscutelor în părțile drepte ale ecuațiilor, adică în conturul EMF.

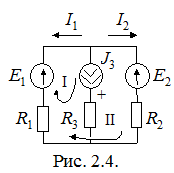
Exemplu. Pentru circuitul din Fig. 2.4

Apoi, sistemul de ecuații prin metoda curenților de buclă ia forma:

Și. Având în rezolvat prima ecuație poate fi obținut. mai departe

UJ poate fi determinată din al doilea sistem de ecuații sau egala II pe legea lui Kirchhoff pentru orice circuit care include o sursă de curent.