Noi găsim ecuația parametrilor de regresie liniară și coeficientul de a da o interpretare economică

1. Găsiți parametrii ecuației de regresie liniară pentru a da o interpretare economică a coeficientului de regresie.

2. Se calculează resturile; găsi suma reziduală a pătratelor; estimează reziduurile de varianță; complot reziduurile.

3. Verificați performanța ipotezelor OLS.

4. Se efectuează prin semnificația parametrilor ecuației de regresie folosind testul t al lui Student (# 945 = 0,05).

5. Se calculează coeficientul de determinare, testați semnificația ecuației de regresie folosind F - criteriul Fisher (# 945 = 0,05) pentru a găsi eroarea relativă medie de aproximare. Pentru a trage o concluzie cu privire la calitatea modelului.

6. Punerea în aplicare a predicția valorii medii indicatorului Y la un nivel de semnificație # 945; = 0,1, în cazul în care valoarea estimată a factorului X este de 80% din valoarea sa maximă.

7. Furnizarea unui model grafic și valoarea reală a punctului Y predicție.

8. Scrieți ecuațiile de regresie neliniară și de a construi programele lor:

9. Pentru aceste modele pentru a găsi coeficienții de determinare și eroarea medie relativă de aproximare. Comparați modelele acestor caracteristici și pentru a trage o concluzie.

Noi găsim parametrii ecuației de regresie liniară și a da o interpretare economică coeficientul de regresie.

ecuația de regresie liniară are forma:

Calculele pentru găsirea parametrilor a și b sunt prezentate în tabelul 2.

Valorile calculate pentru găsirea parametrilor ecuației de regresie liniară.

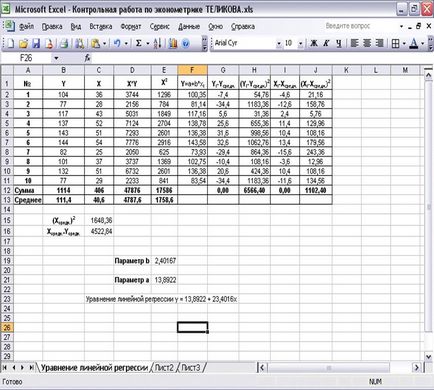
ecuația de regresie este: y = 13,8951 + 2,4016 * x.

Odată cu creșterea volumului de investiții (X) până la 1 mln. Frecați. volumul producției (Y) va crește cu o medie de 2,401,600 ruble .. Astfel, există dovezi ale unei corelații pozitive, indicând faptul că eficiența întreprinderilor și rentabilitatea investițiilor în activitățile lor.

2. Se calculează reziduurile; găsi suma reziduală a pătratelor; Am construi o variatie de estimare a reziduurilor grafic ostatkovi.

Suma reziduală a pătratelor abaterilor: = 207.74.

reziduuri de dispersie: 25.97.

Calculele sunt prezentate în tabelul 3.

Graficul reziduuri are forma:

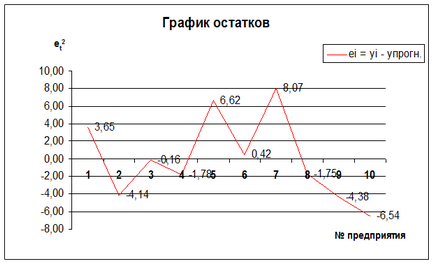
Fig.1. reziduuri Program

3. Verificați dacă premise MNC care cuprinde elementele:

- verificarea egalității așteptarea componentei aleatoare la zero;

- natura aleatorie a reziduurilor;

- conformitatea cu un număr de ramasite ale legii normale de distribuție.

Verificarea egalității nivelurilor așteptarea unui număr de solduri la zero.

Realizarea în timpul auditului H0 ipoteza nulă corespunzătoare:. În acest scop a construit t-statistici. în cazul în care.

. Astfel, ipoteza este acceptată.

Natura aleatorie a reziduurilor.

Vom verifica numărul de resturi de niveluri aleatoare întorcând criterii puncte:

Numărul de puncte de rotație este determinată din tabelul de reziduuri:

= 6> [4.3029], prin urmare, proprietatea resturilor Randomness executate.

Independența reziduurilor este verificată folosind testul Durbin - Watson:

Din moment ce a căzut în intervalul de la d2 la 2, atunci acest criteriu poate concluziona cu privire la punerea în aplicare a proprietăților de independență. Acest lucru înseamnă că un număr de vorbitori nu există autocorelație, astfel încât modelul este adecvat pe acest criteriu.

Reziduuri din seria Value distribuție normală este determinată folosind R / S criterii pentru nivelurile critice (2.7-3.7);

Se calculează valoarea RS:

unde Emax - numărul maxim de nivele de E rezidual (t) = 8,07;

emin - numărul minim de niveluri Reziduuri E (t) = -6,54.

S - abaterea standard = 4.8044.

Deoarece 2.7<3,04<3,7, и полученное значение RS попало в за-данный интервал, значит, выполняется свойство нормальности распределения.

Astfel, luând în considerare diferitele OLS criterii de performanță ipoteze vin la concluzia că sunt îndeplinite condițiile prealabile OLS.

4. să verifice semnificația parametrilor ecuației de regresie folosind testul t Student # 945; = 0,05.

Testarea importanței coeficienților de regresie individuali, asociați definiția valorilor calculate testul t (t-statistici) pentru coeficienții de regresie respectivi:

Apoi, valorile calculate sunt comparate cu ttabl intabulate = 2.3060. Valoarea tabular criteriu determinat de (n- 2) grade de libertate (n - numărul de observații), iar nivelul de semnificație corespunzătoare a (0,05)

Dacă valoarea calculată a testului t cu (n-2), Bauds sale grade mai mare decât valoarea sa de masă, la un anumit nivel-ZNA chimosti, coeficientul de regresie este considerat semnificativ.

În acest caz, coeficienții de regresie a0 - nesemnificativ, a1 - coeficienții semnificativi.

5. calcula coeficientul de determinare, verifică semnificația ecuației de regresie cu criteriul Fisher pomoschyu-, ​​găsim o eroare relativă medie de aproximare. Pentru a trage concluzii cu privire la calitatea modelului.

Definim un coeficient liniar al perechii de corelare, conform formulei

Se calculează coeficientul de determinare:

Aceasta arată variația fracției efective a caracteristică, sub influența factorilor investigați, și anume Ea determină cât de mult din variația lui Y este luată în considerare în modelul și datorită influenței factorilor pe ea.

Cu cât R 2 la 1, cu atât mai bine calitatea modelului.

Variația rezultat Y (volumul producției) până la 96,8% a explicat factor de variație X (volum expansion capitale).

Evaluarea semnificației ecuației de regresie pentru a ține Pomo-schyu Fisher F-test:

Ecuația de regresie cu o probabilitate de 0,95 în general STATIS-semnificative de vedere genetic, adică. A. F> Ftabl.

Definim medie aproximarea eroare relativă:

valorile medii calculate pentru modelul-y liniară a valorilor reale diferă de la 3.863% la

Deoarece eroarea de aproximare a modelului este mai mică de 7%, indică bun ca model.

6. Realizăm medie nivelul de semnificație pokazatelyapri predicție, în cazul în care valoarea estimată a factorului Hsostavit 80% din valoarea sa maximă.

Valoarea predictivă a indicelui, în cazul în care valoarea estimată a factorului X este de 80% din valoarea sa maximă de 0,8 * 54,00 = 43,20, va fi:

y f-cast = + 2,40 * 13.89 43.20 = 117.64.

pentru grade de libertate și un nivel de semnificație de 0,1 este egal cu 1.8595.