Operații cu vectori în coordonate

Cu vectorul definit într-un sistem dreptunghiular pentru a efectua acțiuni chiar mai ușor decât cu imaginile lor geometrice de coordonate. In acest articol vom arăta cum să efectueze operațiile de adunare a vectorilor și multiplicarea unui vector de un număr, dacă știi coordonatele lor și să analizeze în detaliu soluțiile de exemple.

Să planul definit de coordonate cartezian rectangular sistem Oxy. Luați în considerare vectorii. Acești vectori pot fi descompuse de coordonate vectorii și altele asemenea, care a fost demonstrat în articol vectorului coordonatelor într-un sistem de coordonate carteziene.

Găsiți suma vectorilor, precum și produsul unui vector de către orice număr real.

Prin proprietățile operațiilor asupra vectorilor. avem următoarea egalitate

Laturile drepte ale acestor ecuații reprezintă vectori și extinderea coordonatelor vectorilor și în consecință, vectorii au coordonate și, respectiv.

In mod similar, pentru vectorii definiți într-o formă dreptunghiulară de coordonate Oxyz sistem în spațiul tridimensional, putem scrie

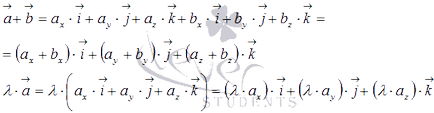
Prin urmare.

Astfel, coordonatele și suma vectorială egal cu vectorii sumă și coordonatele corespunzătoare,

și coordonatele produsului vectorial al numărului egal cu coordonatele corespunzătoare ale vectorului, înmulțit cu un număr predeterminat într-un sistem de coordonate.

Dacă doriți să găsiți coordonatele unei sume a mai multor vectori, acestea vor fi egală cu suma coordonatele corespunzătoare ale fiecăruia dintre vectori.

Să examinăm câteva exemple de soluții.

Efectuați operația de adăugare și vector precum și obține coordonatele produsului vectorial al numărului.