Panta liniei tangente
Dacă funktsiyaimeet derivat finit în tochketo în okrestnostieo poate priblizitlineynoy funcție
Q tochkeChisloyavlyaetsya Funktsiyanazyvaetsya panta tangentei sau linia tangensomuglanaklonakasatelnoy.
Rata funcției schimbare
legea pryamolineynogodvizheniya Pust-. Togdavyrazhaetmgnovennuyu skorostdvizheniya când vremeniVtoraya accelerare proizvodnayavyrazhaetmgnovennoe punct în timp
În general, derivat funcția tochkevyrazhaet funcția de schimbare a vitezei, la punctul, adică protekaniyaprotsessa viteză descrisă dependența
19 derivați ai Properties. reguli de diferențiere
Funcția având un derivat finit (la un moment dat), se face referire la diferenția (în acest moment).
Proprietățile de bază ale funcțiilor derivate (două tabele de Shipacheva și de pe Internet)

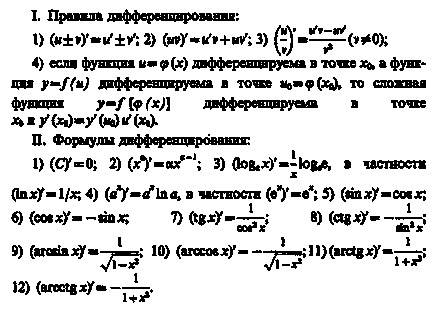
20 Derivata funcții elementare.

21 Derivata unei funcții compozit. Derivata funcției inverse
Derivata funcției compozit
Eslifig- funcția diferențiabilă, atunci funcția compozit este diferențiabilă și derivatul său este poxi
Această formulă arată că funcția compozit derivat egal cu produsul funcției derivat al exteriorului derivat al funcțiilor interioare. Este important să se țină cont de faptul că derivata funcției interioare evaluate la x, iar derivata funcției exterioare - în tochkeu = g (x)!
Se poate observa că funcția compozit derivat este reprezentat ca un produs de serie funcții constitutive derivate, argumentele funcționale aliniate (legat), astfel încât valoarea funcțiilor interne ale unui argument pentru următoarea funcție de ei externă. Prin urmare, regula pentru diferențierea unei funcții compozit este adesea numită „regula de lanț“ (regula de lanț).
Derivata funcției inverse
Funcția Pust- a argumentului x la un anumit interval. Dacă uravneniiy ca un argument, și x - funcție, există o caracteristică nouă în cazul în care funcția inversă.
Pentru funcția diferențiabilă cu un alt derivat de la zero, derivat inversul de feedback funktsiiravna al derivatului acestei funcții, și anume
22 Funcția diferențialului. Semnificația geometrică
Differential (diferență otlat.differentia-, diferența) - funcție liniară chastprirascheniya.


În funcțiile grafic vom lua un arbitrar tochkui da argumentupriraschenie. Funcția primește incrementul (în segmentul de imagine).
Desenați o tangentă la curba de la punctul notat cu unghiul de înclinare față de osicherez atunci. De la treugolnikanahodim, și anume ..
Astfel, numeric egală cu creșterea differentsialfunktsii ordoneze tangenta la graficul funcției în punctul în care argumentpoluchaet incrementat.