Portalul Educațional Tsu

Modulul 3 este format din două conferințe, în care următoarele aspecte:

1. Cinematica și solid.
2. Cinematica,
3. Introducere în cinematică.
4. Metode de specificare punct mișcării.
5. Viteza Vector unui punct.
6. Punctele vectorului accelerație.
7. Determinarea vitezei și accelerației punctului în coordonate mișcare metoda punctului de atribuire.
8. punctul tangențiale de accelerare și normală.
9. Unele cazuri speciale de mișcare a unui punct.
10. mișcare de translație și de rotație a unui corp rigid.
11. mișcare translațională.
12. mișcare rotațională a unui corp rigid în jurul unei axe.
13. viteza unghiulară și accelerația unghiulară.
14. Rotatie uniforma si ravnoperemennoe.
15. Viteza și accelerația punctelor corpului rotativ.

Studiul acestor probleme trebuie să fie în continuare la dinamica de mișcare a unei particule, dinamica mișcării relative a punctului, dinamica mișcării de rotație a unui punct, pentru a rezolva problemele din disciplinele „Teoria mașinilor și mecanisme“ și „piese Machine“.

Cinematica și solide

Introducere în cinematică

• Chemat cinematica ramură a mecanicii care studiaza proprietatile geometrice ale mișcării corpurilor, indiferent de inerția (masă) și forțele care acționează asupra lor.
• Sub mișcare, înțelegem mecanismul de schimbare, cu trecerea timpului poziția corpului în spațiu în raport cu alte organisme.
• Pentru a determina poziția corpului în mișcare (sau puncte), la momente diferite, cu corpul, în raport cu care mișcarea este studiată în mod rigid leagă orice sistem de coordonate care formează împreună cu cadrul corpului de referință.
• noi reprezentăm un cadru de referință sub forma a trei axe (fără a arăta corpul cu care sunt asociate).
• Mișcarea corpurilor în spațiu se face în timp. Spațiul în mecanica, considerăm modul în care spațiul euclidian tridimensional.

Timpul este un scalar, în continuă schimbare magnitudine. Sarcinile cinematicii timpul t este luată ca variabilă independentă (argument). Toate celelalte variabile (distanța, viteza și așa mai departe. D.) sunt considerate ca schimbare a lungul timpului t, e. Ca o funcție de timpul t.

Pentru a rezolva problemele cinematice este necesar să se studieze mișcarea a fost oarecum stabilită (descrisă).

set Cinematografic mișcării sau mișcarea legii a corpului (puncte) - înseamnă a specifica poziția corpului (puncte) în raport cu un sistem de referință dat la un moment dat.

Sarcina principală a cinematicii și solide este de a cunoaște legea mișcării punctelor (corp), pentru a stabili metode pentru determinarea cantităților cinematice ce caracterizează această mișcare.

Metode de specificare mișcării punctului

una dintre următoarele trei metode pot fi folosite pentru a seta deplasarea punctului:

1) un vector, 2) coordonează, 3) naturale.

1. Metoda Vector de specificare a mișcării unui punct.

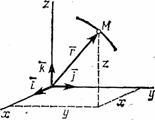
Să punctul M se deplasează în raport cu un sistem de referință Oxyz. Poziția acestui punct, în orice moment dat poate fi determinat prin specificarea r său vector raza, trasată de la originea O la un punct M (fig. 1).

Deoarece punctul M, vectorul va modifica în timp și în magnitudine și direcție. Prin urmare, un vector variabil (funcția vector), în funcție de argumentul t.

Egalitatea definește legea punctelor de mișcare într-o formă de vector, deoarece permite, în orice moment pentru a construi un vector adecvat și de a găsi poziția unui punct în mișcare.

Locus tuturor vectorilor t. E. izvor de falie al vectorului, determină traiectoria unui punct în mișcare.

2. Referința de coordonate mod punct de mișcare.

Poziția poate fi determinată în mod direct punctul divid prin coordonatele carteziene x, y, z, care atunci când punctul se deplasează vor varia în timp. Pentru a cunoaște legea mișcării punctului-zheniya T. Poziția E. ei în spațiu, în orice moment dat, este necesar să se cunoască valorile coordonatele fiecărui punct în timp, t. E. În funcție de know

Ecuațiile sunt ecuațiile de mișcare a unui punct în coordonate carteziene. Acestea definesc legea mișcării punctului cu metoda de coordonate a sarcinilor de mișcare.

3. Calea naturală de a specifica punctul de mișcare.

mod natural de sarcini de mișcare este convenabil de a utiliza, în cazurile în care traiectoria unui punct în mișcare este cunoscut în prealabil. Lăsați curba AB este traiectoria M deoarece se deplasează în raport cu Oxyz cadru (Figura 2) Am ales această cale un anumit punct O fix“, care este luat ca punct de referință, și a stabilit pe traiectoria direcțiilor pozitive și negative ale referinței (ca pe o coordonată axa). Apoi, poziția punctului M pe traiectoria curbilinie Coordonata-Nata este unic determinată s, care este egală cu distanța de la punctul O „la punctul M, măsurată de-a lungul arcului traiectoriei, și a luat cu semnul corespunzător.

Atunci când se deplasează punctul M se deplasează în poziția M1, M2. prin urmare, distanța s va varia în funcție de timp.

Pentru a cunoaște poziția punctului M pe calea la un moment dat, este necesar să se cunoască dependența

Ecuația exprimă legea de mișcare a punctului M de-a lungul unui traseu.

Viteza Vector a unui punct

Una dintre principalele caracteristici ale punctului de mișcare TION cinematic este o mărime vectorială numită punctul de viteză. Prezentăm mai întâi conceptul de viteza medie a punctului pentru o anumită perioadă de timp. Să punctul în mișcare este

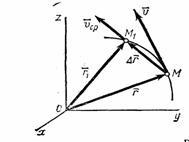
la momentul t la poziția M definită de un vector r raza, iar timpul t1 vine în poziția definită de vectorul M1 (Figura 3). Apoi mișcarea punctului timpul definit intervalul de vectorul pe care o numim un puncte vector de mișcare. văzut din OMM1 triunghi; Prin urmare.

Raportul dintre punctele vectorului de mișcare la intervalul de timp corespunzător, furnizează o cantitate vectorială numită viteza media modulo și puncte de direcție, în intervalul de timp.

Punct Rate la un moment dat t este o valoare vector v, care tinde sa medie a vitezei intervalului Vav tinde la zero:

Astfel, viteza vectorială a unui punct într-un moment dat este egal cu un prim derivat al vectorului de raza la un moment de timp.

Deoarece secantă limita MM1 direcție este tangent, vectorul vitezei unui punct într-un timp dat este direcționat de-a lungul tangenta la traiectoria unui punct în direcția de deplasare.

Punctele vectorului accelerație

Punct Accelerația este o mărime vectorială care caracterizează schimbarea peste unitatea de timp și direcția punctelor de viteză.

Să presupunem că la un anumit moment t punctul în mișcare este în poziția M și are o viteză v, iar timpul t1 vine la poziția M1 și are viteza V1 (Fig. 4). Apoi, în timpul intervalului de timp viteza de creșteri de puncte. Pentru a construi un vector dintr-un punct M amâne vector egal cu v1 și construi un paralelogram, in care diagonala este, o latură. Apoi, în mod evident, cealaltă parte va fi reprezentată printr-un vector. Rețineți că vectorul este întotdeauna îndreptată spre traiectoria-WOG nutosti.

Raportul dintre incrementul vectorului de viteză care corespunde unui interval de timp determină vectorul mediu de accelerare a unui punct pentru intervalul de timp:

vector medie accelerație are aceeași direcție ca și vectorul, adică. E. direcționată spre concavitatea traiectoriei.

Punct Accelerația la un moment dat t este o mărime vectorială, care tinde la intervalul mediu timp de accelerare tinde la zero: puncte vector de accelerare la un moment dat este egal cu un prim derivat al vectorului de viteză sau derivata a doua a vectorului de raza la un moment de timp.

Ne găsim, ca locație a vectorului în ceea ce privește traiectoria punctului. In vectorul de mișcare rectilinie este direcționat de-a lungul liniei drepte de-a lungul care se mișcă punctul. Dacă traiectoria unei curbe plane, vectorul accelerație, precum vectorul se află în planul curbei și îndreptat spre concavitatea. Dacă curba traiectoriei nu este plană, vectorul îndreptat spre concavitatea calea și situată într-un plan care trece prin tangenta la traiectoria la punctul M și o linie dreaptă paralelă cu tangenta la punctul adiacent M1 (fig. 4). În limita, atunci când punctul M tinde spre M, acest plan în poziția de așa-numitul plan osculating; avionul în care există o rotație tangentă infinitezimal traiectoria unui deplasare elementară a punctului în mișcare. Prin urmare, în general, vectorul accelerație se află în planul osculating și îndreptat spre concavitatea curbei.

Determinarea vitezei și accelerației în punctul de coordonate metodei de referință al mișcării

1. Determinarea punctului de viteză. Vectorul de viteză a punctului, având în vedere că am găsit:

Astfel, viteza de proiecție a unui punct de pe axele de coordonate sunt egale cu un prim derivat al coordonatelor corespunzătoare ale punctelor de timp.

Știind proiecția vitezei găsi magnitudinea și direcția sa (adică, unghiurile care formează un vector v cu axele de coordonate) cu formulele

2. Determinarea punctului de accelerație. Punctele vector de accelerare în proiecția pe axa obținem:

și anume punct de proiecție accelerare pe axe de coordonate egală cu prima derivată a vitezei proeminențelor sau derivata a doua coordonatele corespunzătoare ale punctelor de timp. Amploarea și direcția accelerației se găsesc din formulele

unde - unghiul format de vectorul accelerație cu axele de coordonate.

Astfel, valoarea numerică a vitezei punctului în acest moment este prima derivată a distanței (coordonate curbilinii) s-un punct în timp.

Vectorul de viteză este direcționat de-a lungul tangentei la calea, pe care am cunoscut dinainte.

punctul tangențiale de accelerare și normală

Cu mișcare naturală proces de alocare vector este determinat prin proeminențele sale la axa b M n. având un început la punctul M și se deplasează împreună cu ea (Fig.5). Aceste axe sunt numite axe (sau axe ale vitezei) triedru naturale, regia urmează: axa - de-a lungul tangenta la traiectoria din distanța de referință pozitivă s; Axa M n - culcată normală în planul osculating și îndreptat spre traiectoria concavă; Axa M n - perpendicular pe primele două, astfel încât să fie ia format cu un dreptaci. M n Normal. situată în planul osculating (în planul curbei în sine, în cazul în care curba este plat), denumit principal normal și perpendicular pe acestea o M normală b - binormal.

S-a arătat că punctul de accelerație se află în planul osculating, adică într-un plan ..; prin urmare, proiecția pe vectorul binormal este zero ().

Calculăm proiecția pe celelalte două axe. Să presupunem că la momentul t punct se află în poziția M și o viteză v, un moment sosește în poziția M1 și are o viteză v1.

Apoi, prin definiție,

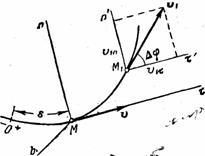
Procedăm în această ecuație din vectori proeminențele lor pe axa, efectuată la punctul M (Fig.5). Apoi, pe baza teoremei sumei de proiecție (sau diferența) a vectorilor pentru a obține axa:

• Având în vedere că proiecția vectorului pe aceleași axe paralele, prin punctul de M1 axele paralele și reprezintă unghiul dintre vectorul de direcție și tangenta prin. Unghiul dintre tangenta la curba la punctele M și M1 numit unghi de adiacenta.
• Să ne amintim că relația adiacenta unghiul limită pentru lungimea arcului determină curbura k a curbei în punctul M. Curbura este reciproca a razei de curbură în punctul M. Astfel,

• Revenind acum la desen (Figura 6), constatăm că proiecțiile vectorilor și sunt axe egale,

în care v și v1 - valoarea numerică a punctului de viteză la t și t1 Instants.

Rețineți că punctul M1 infinit mai aproape de M și, în același timp.

Apoi, având în vedere că, în limita, obținem expresia

Partea dreaptă a expresiei AN transforma, astfel încât acesta a inclus relația, dincolo de care ne sunt cunoscute. Pentru a face acest lucru, se înmulțește numărătorul și numitorul fracției sub semnul limită pentru. Apoi, avem

deoarece limitele fiecăruia dintre factorii din paranteze sunt atunci când:

Astfel, am arătat că proiecția punctului de accelerație pe o tangentă egală cu un prim derivat din valoarea numerică a vitezei sau derivata a doua a distanței (coordonate curbilinii) e timp și proiecția accelerației la principala normală este egală cu pătratul vitezei împărțită la raza de curbură a traiectoriei la un anumit punct al curbei; accelerare proiecție binormal este zero (ab = 0). Aceste rezultate din el unul dintre cele mai importante teoreme ale cinematicii oferă.

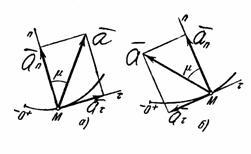
Amînarea lungul tangentei și vectorii principali normali și Mn, și numeric egală cu o (fig. 6). Acești vectori reprezintă tangenta și componentele normale ale punctului de accelerație. Atunci când această componentă este întotdeauna îndreptată spre concavitatea curbei (valoarea unei „este întotdeauna pozitiv), iar componenta poate fi direcționată sau într-o direcție pozitivă sau negativă în funcție de axa mărcii de proiecție (vezi. Fig. 6a și b).

Vectorul accelerației este reprezentat printr-un punct diagonal al paralelogramului construit pe componentele și. Deoarece aceste componente sunt reciproc perpendiculare, Mod:

Unele cazuri speciale de mișcare a unui punct.

Folosind rezultatele obținute, considerăm unele cazuri particulare de mișcare a unui punct.

1. drepte. În cazul în care punctele de cale este o linie dreaptă, atunci. Apoi, tot punctul de accelerație este egală cu o accelerație numai tangențială:

Deoarece, în acest caz, se modifică viteza de numai numeric, putem concluziona că tangenta caracterizează viteza de accelerare a schimbării valorii numerice.

2. uniform mișcarea curbilinie. Uniforma numit o mișcare curbilinie a unui punct în care valoarea numerică a vitezei rămâne constantă în orice moment:

v = const. Apoi, tot punctul de accelerație este egală cu una normală numai:

Vectorul accelerație este îndreptată în același timp, toate normale la traiectoria punctului.

Deoarece, în acest caz, accelerația apare doar prin schimbarea direcției vitezei, putem concluziona că accelerația caracterizează viteza de schimbare de direcție. Noi găsim legea de mișcare curbilinie uniformă.

Din formulă avem.

Să presupunem că la momentul inițial (t = 0) este punctul de origine în s0 regiune. Apoi, luând de pe partea stângă și dreaptă a integralele definite în măsura în care este necesar, se obține

deoarece v = const. În cele din urmă vom găsi legea de mișcare curbilinie uniforme sub forma

Dacă s0 = 0, atunci s va da drumul parcurs de momentul de timp t. Ca urmare, în calea mișcării uniforme traversate de punctul de calcul proporțional timp, o viteză relativă cale de mișcare este egal cu timpul

3. uniform mișcării rectilinii. În acest caz, și, prin urmare, a = 0. Rețineți că singura mișcare în care accelerația punctului este zero, în orice moment, o mișcare liniară uniformă.

4. Ravnoperemennoe mișcare curbilinie. Ravnoperemennym numit o mișcare curbilinie a unui punct în care accelerația tangențială este menținută constantă :. Noi căutăm legea de mișcare, presupunând că la t = 0

s = s0, și v = v0, în care v0 - viteza punctului inițial. Conform formulei avem.

Din moment ce, atunci, luând din ambele părți ale ultima egalitate integrală în măsura în care este necesar, obținem:

Formula poate fi reprezentat ca

O a doua integrare, vom găsi legea ravnoperemennogo mișcare curbilinie a unui punct

În cazul în care mișcarea curbilinie a punctului crește modulul de viteză, mișcarea se numește accelerație, și scade în cazul în care - cu întârziere.