Proprietatea diagonalele unui paralelogram

Proprietatea diagonalele unui paralelogram

Teorema 6.2 (invers Teorema 6.1). diagonalele de paralelogram se intersectează și punctul de intersecție sunt împărțite în jumătate.

Dovada. Să ABCD - paralelogramului (Figura 120.). Va deține BD său pe diagonală. Notă cu privire la aceasta cu privire la mijloc și pe extinderea segmentului AB amâne OC1 segment. egală cu AB.

Teorema 6.1 ABC1 D patrulater este un paralelogram. Prin urmare, o paralelă directă cu BC1 AD. Dar prin punctul B poate fi realizată doar o singură linie paralelă cu AD. Deci, BC1 drept coincide cu linia BC.

În mod similar, se dovedește că linia DC1 coincide cu linia de curent continuu.

Prin urmare, un punct C1 coincide cu punctul C coincide cu paralelogramul ABCD ABC1 D. Prin urmare, diagonalele sale se intersectează și punctul de intersecție sunt secționate. Acest lucru dovedește teorema.

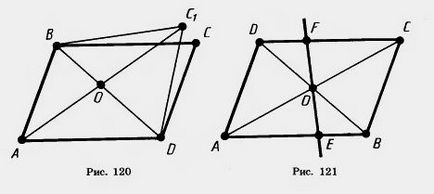
Problema (6). Prin diagonalele paralelogramului punctul de intersecție al liniei drepte. Dovedește că lungimea lui, a intrat în între laturile paralele, este împărțit în jumătate de acest punct.

Decizie. Să ABCD - EF paralelogram - intersectând linia laturile paralele AB și CD (Figura 121.). Triunghiuri OUA și sunt EFE al doilea semn. Ei mână OA și OC sunt egale, deoarece G - AC diagonală de mijloc. Unghiurile de la vertex O sunt atât pe verticală, iar unghiurile JAR și FCO sunt ambele paralele interne cruce culcat cu AB, CD și divizat AC.

Din egalitatea triunghiurilor ar trebui să fie egalitatea armelor: OE = A, după cum este necesar.

A. V. Pogorelov, Geometrie pentru clasele 7-11, manual pentru instituțiile de învățământ

Planificarea lecții în matematică on-line. provocări și răspunsuri în clase, clasa de matematică temele 8 descărcare

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.