Selectarea secțiunea dreptunghiulară - sopromat - Articole Director
Lucrările de decontare și grafice au nevoie pentru a ridica secțiunea transversală de formă dreptunghiulară.
In starea ne sunt date raportul de aspect dreptunghi β = h / b. efort admisibil normale [σ] și o tensiune de forfecare admisibil [τ]. Nu vom intra în teoria pentru soluții nu este nevoie de mare, totul este rezolvat prin formule elementare.
In toate exemplele de realizare ne-a dat:
Dar, β, în toate formele de realizare diferite, vom lua β = 2.3
Provocarea este de a găsi laturile dreptunghiului, se calculează tensiunile maxime și să le compare cu permis. Mai departe.
Există o formulă a momentului de rezistență dorită:
formula generală pentru momentul rezistenței
este dată de momentul de inerție pentru un dreptunghi:
Un audio Zmax altul decât jumătate din lungimea h
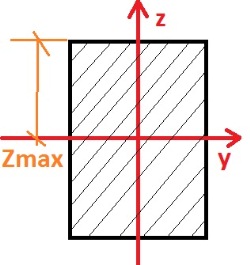
Din această formulă devine un fel:
poate fi exprimată într-o direcție de raportul dintre părți, prin cealaltă, de exemplu, exprimă h
Acum substituie aceasta în formula h obținut mai sus momentul rezistentei Wy
Din moment ce înregistrăm
Mmah ne uităm la diagramele noastre, care este valoarea maximă a punctelor.
Prin urmare, ne exprimăm b
Înlocuim valoarea M. în lecțiile anterioare, în cazul în care am rezolvat fasciculul și de a construi diagrame Mmah = 16 kN * m
Dar, trebuie să respecte dimensiunea, deoarece [Σ] în MPa.
16 kN * m = 16 * 10 -3 Mpa * m 2
Înlocuim valoarea în formulă și pentru a obține răspunsul:
Noi găsim raportul de aspect al h
Acum. când am găsit cele două părți ale dreptunghiului, avem nevoie pentru a calcula momentul de rezistență Wy
Putem determina acum valoarea reală a tensiunii normale:
Am calculat de tensiune. Acum trebuie să le construiască epure
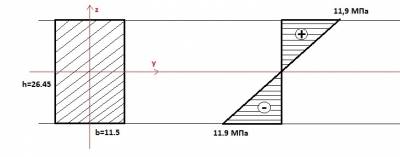
Așa cum arată diagrama. Ce este în valoare de vedere: în mijlocul unei tensiuni egal cu 0, la ambele capete ale maxime și acestea sunt egale cu 11,9 - adică, am găsit valoarea. Care sunt semnele + și - în diagramele noastre? În calculele am folosit cuplul maxim, și este în valoare de un aspect cu care el era familiar. În cazul în care semnul este pozitiv - aceasta înseamnă că fasciculul în această secțiune
Acesta este îndoit în așa fel

Dacă rezultatul este negativ, prin aceea că
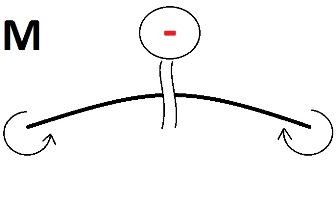
Am avut un moment este -16, iar fasciculul în această secțiune ia forma prezentată în cea de a doua figură.
Aceasta înseamnă că fibrele superioare sunt întinse și inferior comprimat (aceasta se poate vedea în figură). Când lungimea intinsa de fibre creste, compresiune - scade. De fapt, pe diagrama indicăm în ce loc ne-am intins fibre - un semn plus, și în care comprimat - semnul minus.
În continuare avem nevoie pentru a verifica rezistența tensiunilor fasciculului de forfecare.
În acest scop, grinzi noastre din lecțiile anterioare trebuie să învețe Qmax maximă forță transversală.
Ei putem vedea pe diagrama, pe care am construit în lecția.
Destul de ciudat, dar forța laterală maximă, precum și de timp, este egal cu 16kN.
Există o formulă specială de calcul:
Aceasta este, tensiunea maximă de forfecare trebuie să fie mai mică decât admisibilă.
Înlocuim valorile noastre, ținând cont de dimensiunea
0,79 MPa mai puțin decât admisibilă 2 MPa.
Și acum trebuie să construim eforturi de forfecare epure. Este mai ușor decât diagrama de tensiuni normale, deoarece nu este necesar să se ia în considerare fasciculul este întinsă sau comprimată, ceea ce înseamnă că nu există nici un hassle cu semne.
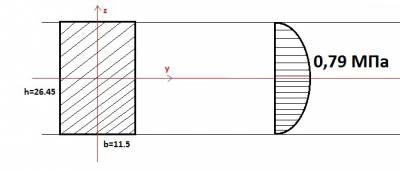
Diagrama reprezintă ceva de genul unui arc. La capetele stresului de forfecare este egal cu 0, iar în mijloc este maximă și egală cu valoarea găsită de noi.
Astfel, am ales pentru grinzi noastre dreptunghiulare, am găsit o tangentă și tensiunii normale în secțiunea transversală și a construit diagrame lor.