Seria Fibonacci - un
origine
Secvența Fibonacci a fost bine cunoscut în India antică, în cazul în care a fost folosit în științe metrice (prozodie, cu alte cuvinte - prozodie), cu mult înainte de a devenit cunoscut în Europa.
Proba de lungime n poate fi determinat prin adăugarea la proba S n-1 în lungime. sau lungimea L a eșantionului n-2; și prosoditsisty a arătat că numărul de eșantioane de lungime n este suma celor două numere anterioare din secvență. Donald Knuth consideră că acest efect în cartea „Arta calculator de programare“.
În Occident, această secvență a fost studiată de Leonardo din Pisa, cunoscut sub numele de Fibonacci, în lucrarea sa «Liber Abaci» (1202). El consideră că dezvoltarea unei (biologic nerealistă) populație de iepure idealizate, presupunând că:
- In luna „zero“, există o pereche de iepuri (0 noi cupluri).
- În prima lună, prima pereche dă naștere la o altă pereche (1 pereche nouă).
- În a doua lună, cele două perechi de iepuri au alte cupluri și prima pereche de matrițe (1 pereche nouă).
- In luna a treia, a doua pereche, și două perechi noi de a genera un total de trei perechi de noi și vechi a doua pereche de matrițe (2 perechi noi).
Natural este faptul că fiecare pereche de iepuri produce încă două perechi de viață, și apoi mor.
Lăsați populația în ultima lună n va fi egal cu F (n). În acest moment, numai iepurii care au trăit în luna n-2 sunt capabile de reproducere și de a produce urmași, atunci F (n-2) perechi vor fi adăugate la populația actuală a F (n-1). Astfel, numărul total de perechi este egal cu F (n) = F (n - 1) + F (n - 2).
Formula lui Binet
Binet formula exprimă în mod explicit valoarea Fn ca funcție de n:
,
în cazul în care - secțiunea de aur. În același timp, și sunt rădăcinile unei ecuații pătratice.
Din formulele Binet rezultă că pentru toți, au cel mai apropiat întreg Fn. adică. În special, asymptotics.
Și cu formula mai generală:
- Numerele lui Fibonacci sunt prezentate pe un set de valori de unități continuant: adică,
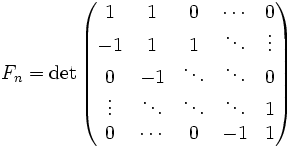
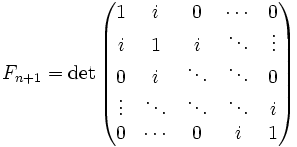
- Numerele Fibonacci pot fi exprimate în termeni de Cebîșev:
- Pentru orice n,
- Corolar. Calculul determinanților dă
- Cel mai mare divizor comun a două numere este egal numarul Fibonacci Fibonacci cu indicele egal cu cel mai mare divizor comun al indicilor m. F. (fm, Fn) = F (m, n). consecinţe:
- Fm este împărțită Fn dacă și numai dacă m este împărțit de n (cu excepția n = 2). In particular, Fm este împărțit de F3 = 2 (adică, este chiar) numai pentru m = 3k; Fm este împărțit de F4 = 3, numai pentru m = 4k; Fm este împărțit de F5 = 5 numai pentru m = 5k și t. D.
- Fm poate fi simplu pentru simplu m (cu singura excepție de m = 4) (de exemplu, numărul 233 este simplu, iar indicele de 13, de asemenea, este simplu). Reciproca nu este adevărat, primul contraexemplul -. Nu se cunoaște dacă setul de numere Fibonacci este infinit, este simplu.
- secventa Fibonacci este un caz particular al secvenței de întoarcere, polinom caracteristic x 2 - x - 1 și are rădăcini.
- Relațiile sunt fracțiile adecvate de aur φ secțiune și, în particular.
- Cantități coeficienți binom de triunghiul lui Pascal pe diagonalele sunt Fibonacci vedere formula
- . 1964 J. Cohn (Jhe Cohn) a demonstrat că numai pătrate perfecte între numere Fibonacci sunt numere Fibonacci de indexuri 0, 1, 2, 12: F0 = 0 2 = 0. F1 = 1 2 = 1. F2 = 1 2 = 1. F12 = 12 februarie = 144. În acest caz, pentru n = 0,1,12 declarație true Fn = n 2.
- Generarea funcție a secvenței Fibonacci este:
- O multitudine de numere Fibonacci coincide cu setul de valori pozitive ale polinomului
z (x, y) = 2xy 4 + x 2 y 3 - 2x 3 y 2y 5 - x 4 y + 2y,
pe platourile de numere întregi x și y [2].
- Produs și raportul dintre oricare două numere Fibonacci diferite diferite de unitate, nu un număr Fibonacci.
- Numerele recente Fibonacci formează o secvență periodică cu perioada de 60 de ani, ultima pereche de numere Fibonacci formează o secvență de perioadă 300, ultimele trei cifre - cu perioada 1500, ultimele patru - cu perioada 15000, ultimele cinci - cu perioada de 150,000, etc ...
Variații și generalizări
- numerele tribonachchi
- Numerele Fibonacci sunt un caz special de secvențe Lucas, și complementele lor sunt numere Lucas.
În alte domenii
Vezi ce „seria Fibonacci“ în alte dicționare:
Numărul Fibonacci - un număr de fracțiuni, în care fiecare fracție ulterioară obținută prin însumarea numărătorul și numitorul celor două fracțiuni anterioare. Este folosit pentru a caracteriza Filotaxie in plante ... Anatomia și morfologia plantelor
Fibonacci - Leonardo Pizansky Leonardo Pisano Born aprox. 1170 ... Wikipedia
numere Fibonacci - elemente Fibonacci secventa 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765 numerice, 10946 ... (secvența A000045 în OEIS), în care fiecare număr succesiv este suma celor două ... ... Wikipedia
Codul Fibonacci - Fibonacci codare numere intregi Radix mixte bazate pe numere Fibonacci F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, etc. numărul de înregistrare din Codul 0 Fibonacci FSS ...... 0 0 F2 = 1 1 ... Wikipedia
Fibonacci codificare - Fibonacci codare numere intregi Radix mixte bazate pe Fibonacci numere F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, etc. numărul de înregistrare din Codul 0 Fibonacci FSS ...... 0 0 F2 = 1 1 ... Wikipedia
șirul lui Fibonacci - secventa lui Fibonacci, o secvență de matematică care fiecare membru este suma celor două precedente. Astfel, în cazul în care termenul n-lea al secvenței este notat xn, atunci întreaga secvență este corect ecuației ... ... Știință și Tehnologie dicționar enciclopedic
Informații Coding - stabilirea corespondenței între elementele mesajului și semnale, folosind la care se poate fixa aceste elemente. B. Să o multitudine de mesaje, iar alfabetul cu simbolurile. Să presupunem că o secvență finită de simboluri numite. cuvânt în ... ... Encyclopedia fizică
Istoria aritmetică - aritmetică. Pinturicchio a pictat. Borgia Apartments. 1492 1495. Roma, palate Vatican ... Wikipedia
- Veche. Alive Crystal. Secțiunea Matricea de Aur. Această carte se concentrează pe cele trei etape principale ale epocii Varsatorului umane și multidimensionale: Transformare, armonizare și tranzițiile. Dacă vorbim despre multidimensionalitatea, mai devreme sau mai târziu, cercetarea noastră ... Citește mai mult Vand pentru 549 de ruble
- Live cristal. Secțiunea Matricea de Aur. Această carte se concentrează pe cele trei etape principale ale epocii Varsatorului umane și multidimensionale: Transformare, armonizare și tranzițiile. Dacă vorbim despre multidimensionalitatea, mai devreme sau mai târziu, cercetarea noastră ... Citește mai mult Vand pentru 549 de ruble
- Află în 30 de secunde. Matematica timp de 30 de secunde. Brown, P. Ultima teoremă, numarul „pi“, seria lui Fibonacci, triunghiul lui Pascal. Desigur, sunteți conștienți de ceea ce se înțelege prin aceste concepte, sau au auzit de ele. Dar dacă poți cuceri toți invitații la petrecere, ... Citește mai mult Vand pentru 496 de ruble