transformare de coordonate

Matricea care definește o transformare liniară depinde de bază. Vom arăta ceea ce este relația dintre matricea dată în diferite baze de transformare una liniară.

Fiind dată o bază e, e „cu T matricea de tranziție:

Presupunem φ este dată de transformare liniară în aceste baze matrici A și A“, respectiv:

(Te) φ = T (eφ) = T (Ae) = (TA) e; A „(Te) = (a't) e; și anume

În cazul în care cel puțin una i = 1 ... n rândul i-lea TA va fi diferit de-al i-lea rând a't, două combinații liniare diferite ale vectorilor e1, e2, ..., en sunt egale între ele, ceea ce contrazice independența liniară a bazei de e .

Prin urmare, TA = a't, unde (deoarece T este nesingular)

A „= TAT ^ -1; A = T ^ -1 * A „* T

Notă: matricea B și C sunt similare în cazul în care C = Q ^ -1 * B * Q, matricea C se obține prin matricea de transformare matrice B Q

Matrix, definind aceeași transformare liniară în diferite baze, sunt similare între ele. Matricea de transformare liniară în φ e bază „obținută prin transformarea matricei bază de conversie matrice e trecerea de la valoarea inițială e“ la bază e.

Exemplu. Găsiți matricea de tranziție

Decizie. Se poate încerca să găsească elementele matricei în mod direct - stabilirea comunicării între rândurile de formula. În acest exemplu particular, nu este foarte dificil de făcut - prima și a patra coloană din matricea deloc evident de atunci. Dar noi urmați calea formală și de a folosi matricea care definește relația pe care o avem dovada teoremei anterioare. Am pus coordonatele vectorilor de bază în coloanele matricelor corespunzătoare:

În exemplul nostru avem:

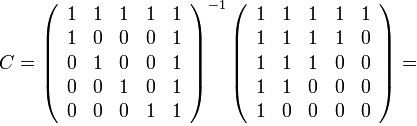
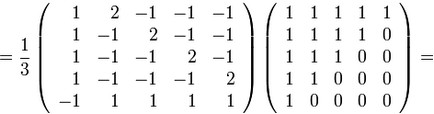
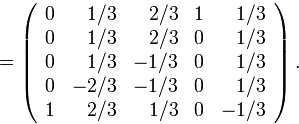
Noile coordonate sunt exprimate în termeni de formula veche

Matricea poate fi interpretată ca matrice a tranziției de la vechiul la noul temei.