Trecerea la o nouă bază

Poort în R are două baze: vechi el. e2. ro și un nou e * l. e2 *. ro *. Orice vector nou bază poate fi reprezentat ca o combinație liniară a vectorilor de bază ale vechiului:

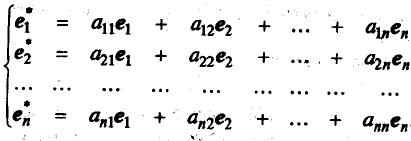
Tranziția de la vechea la noua bază, puteți seta matricea de tranziție

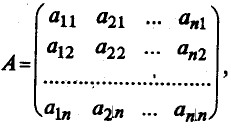
Rețineți că coeficienții de multiplicare ai noilor vectori de bază din vechile coloane formă de bază în loc de rânduri din această matrice.

Matricea A - nesingular deoarece altfel coloanele sale (și, prin urmare, vectorii de bază) să fie liniar dependente. În consecință, are o matrice A inversă -1.

Substituenților în această ecuație valori el *. e2 *. ro * de la sistemul anterior:

Având în vedere independența liniară a vectorilor el. e2. ro toți coeficienții lor în ultima ecuație trebuie să fie zero. De aici:

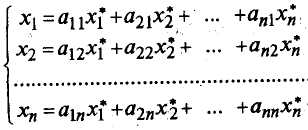
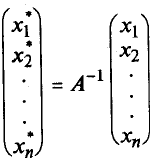
sau sub formă de matrice

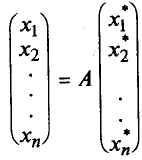
Înmulțind ambele părți de A -1. obținem:

De exemplu, să presupunem că, în baza el. e2. e3 dat vector a1 = (1, 1, 0), a2 = (1, -1, 1), a3 = (-3, 5, -6) și b = (4, -4, 5). Arătați că vectorii al. a2. a3 formează, de asemenea, o bază, și să-și exprime în această bază vektorb.

Noi arată că vectorul Al. a2. a3 sunt liniar independente. Pentru a face acest lucru, vom verifica dacă gradul de o matrice compusă din ele este de trei:

Rețineți că matricea inițială nu este altul decât matricea de tranziție A. De fapt, legătura dintre bazele el. e2. e3 și colab. a2. A3 poate fi exprimată în sistem:

+ 6 = 0 - 3 - 0 - 5 6 + 4 =

operatori liniari

operator liniar (transformare de cartografiere) n-dimensional spațiu vectorial numit praviloY = f (X), prin care fiecare vector X este atribuit un vektorY unic, în care operațiile liniare stocate pe vectori, adică au proprietățile locului:

1) f (X + Z) = f (x) + f (Z) - proprietatea aditivitate operatorului;

2) f (X) = f (X) - proprietate uniformitatea operatorului.

Se poate dovedi că fiecare operator liniar corespunde unei matrice pătrat în această bază. Converse este de asemenea adevărat: Matrix toate operatorul liniar ordine n-lea corespunde spațiu n-dimensional.

De aceea, transformarea liniară poate fi determinată într-un alt mod: operator liniar n-dimensional spațiu vectorial, specificați matrice pătratică A este o transformare care orice vektoruX înregistrată sub forma unei matrice de coloană, se asociază cu vectorul A (X) = A * X =.

O matrice se numește matricea operatorului în această bază, precum și gradul de această matrice este rangul operatorului.

De exemplu, în cazul în care este dat un operator de matrice liniară, apoi otobrazhenieYvektoraX = (4, 3, 1) va fi egal cu

.

Rețineți că matricea de identitate specifică transformarea identității (operatorul de identitate), deoarece prin înmulțirea cu un vector, vom obține același vector.

O matrice zero este definită ca operator de zero. mapează toți vectorii spațiului în vectorul zero.

Este ușor să vă asigurați că matricea diagonală, a cărui diagonală este în valoare de același număr, operatorul stabilește multiplicarea vectorului de acest număr.

Teorema. Matricea A și A * din aceeași linie în baza el. e2. și en el *. e2 *. ro * sunt legate de A = C -1 * AC unde C - o matrice de tranziție de la vechiul la noua bază.

Dovada. Notăm Yotobrazhenie vektoraXv baziseel. e2. ro. și același vector în baza el *. e2 *. ro * X * și semnifica Y *. Deoarece C - matricea de tranziție, putem scrie:

Ne înmulțiți atât pe partea stângă a primei ecuație de matricea A:

Deoarece AX = Y, poluchimY = ACX *. și anume CY * = * ACX. Înmulțind ambele părți ale acestei ecuații cu -1. obținem:

C -1 CY * = C -1 * ACX

Deoarece Y * = A * X *. A = C -1 * AU, după cum este necesar.

De exemplu, să presupunem că, în baza el. e2 matricea A =. Găsiți matricea acestui operator în baza el * = el -2e2. e2 * = 2el + e2.

Pentru aceasta vom construi matricea de tranziție C = și ei matricea inversă C -1 |. C | = 5 ,,. atunci