Trecerea la un alt sistem de coordonate - studopediya

Am analizat transformarea obiectelor geometrice definite într-un anumit sistem de coordonate cartezian. Dar, în multe cazuri, este convenabil să ia în considerare aceleași obiecte din diferite sistem de coordonate, după cum descrierea lor poate fi mai simplu. Cel mai simplu exemplu - o sarcină de coordonate caseta: cel mai simplu mod de a face acest lucru într-un sistem de coordonate, combinat cu unul dintre nodurile sale cu axele dirijate de-a lungul marginilor. În acest sens, vom discuta întrebarea, cum de a schimba coordonatele punctului în tranziția de la un sistem de coordonate cartezian la altul.

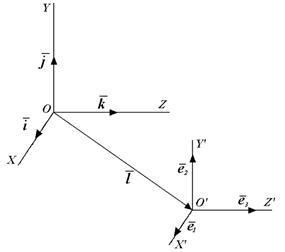
Fig. 3.9. Două sistem de coordonate în spațiu

Să versorii primului sistem de coordonate sunt indicate, iar axele de coordonate -. Vom introduce, de asemenea, un sistem de coordonate, care denotă vectorii unitate, și axe -. Acest sistem își are originea și direcțiile sale axe. Noi credem că, în ambele coordonate vectorii unitate de sisteme formează un triplet stângaci (fig. 3.9).

În primul rând, ia în considerare situația în care punctul coincide cu punctul. Vectorii pot fi definite în primul sistem de coordonate, raspandirea acestora asupra vectorilor:

În cazul în care primul punct are sistem de coordonate, iar al doilea sistem - atunci, în mod evident,

Luând produsul interior, raportul prin vectori, obținem relația dintre valorile coordonatelor în sisteme diferite:

Aceste relații pot fi scrise sub forma de matrice

sau în notație vector

Să presupunem că al doilea sistem de coordonate se obține din prima printr-un unghi de rotație în jurul axei. atunci

Astfel, în viraje noul sistem de coordonate coordonatele punctelor obținute prin înmulțirea matricei de rotație în colțul opus pe coordonatele vectoriale inițiale.

Dacă noul sistem de coordonate se obține prin trecerea de la vechiul vector, este evident că noile coordonate ale unui punct dat de formulele

Acum se poate lua în considerare compoziția a două transformări de coordonate ale sistemului - traducere și de rotație. Apoi, punctele de coordonate transformat de formula