triunghi, teorema lui Pitagora, raportul dintre ipotenuzei și picioarele - geometria

triunghi dreptunghic

Proprietatea. Suma celor două unghiuri acute ale unui triunghi dreptunghic este egală cu 90 0

Proprietatea. Leg triunghi dreptunghiular, situată vizavi de colțul la 0. 30 este jumatate din ipotenuza.

Teorema. Două triunghiuri unghi drept sunt congruente, în cazul în care picioarele sunt egale cu un picior unul față de celălalt.

Teorema. Două triunghiuri unghi drept sunt congruente, în cazul în care ipotenuza și un picior este egal cu ipotenuzei și un picior de altul.

Teorema. Două triunghi dreptunghic sunt egale, dacă unghiul ascuțit și o parte egală cu unghiul ascuțit și de cealaltă parte.

Teorema lui Pitagora

Teorema. Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor celorlalte două laturi.

Teorema, teorema lui Pitagora inversă. Dacă pătratul o latură a triunghiului este egal cu suma pătratelor celorlalte două părți, atunci triunghiul este dreptunghic.

Raportul unui triunghi dreptunghic unghiurile și laturile

Sinusul unui unghi ascuțit al unui triunghi dreptunghic este raportul dintre piciorul opus ipotenuzei.

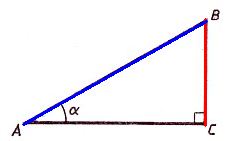
Cosinusul unghiului ascuțit al unui triunghi dreptunghic este raportul dintre piciorul adiacent ipotenuzei.

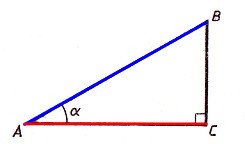
Tangenta unghiului ascuțit al unui triunghi dreptunghic este raportul dintre piciorul opus unui adiacent.

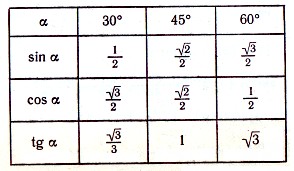
Esențial! ÎNTOTDEAUNA amintesc de ele!

Înălțimea unui triunghi dreptunghic trase din vârful unghiului drept este proporțională cu media între segmente, pentru a împărți înălțimea ipotenuzei.

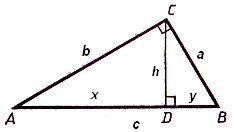
Leg triunghiului dreapta este proporțională cu media dintre ipotenuzei și ipotenuzei segmentului cuprins între picior și înălțimea a avut loc de la vârful unghiului drept.