Unghiul dintre liniile - studopediya
Unghiul dintre liniile drepte în spațiu va fi apelat din orice unghiuri adiacente formate prin două linii trasate prin datele paralele ale unui punct arbitrar.
În spațiul dat două linii:
Este evident că colț # 966; între liniile pot lua unghiul dintre vectorii lor de direcție și. Din moment. formula pentru cosinusul unghiului dintre vectorii obține
.
Termeni paralele și perpendiculare pe cele două linii drepte sunt echivalente cu termenii paralele și perpendiculare pe vectorii lor de direcție și:
Două linii sunt paralele dacă și numai dacă coeficienții corespunzători sunt proporționale, adică l1 l2 paralele dacă și numai dacă paralela.
Două linii sunt perpendiculare dacă și numai dacă suma produselor de coeficienți corespunzători egal cu zero :.
Unghiul dintre linia dreaptă și planul
Să linia D - nu este perpendicular pe planul # 952 ;;
d „- proiecția pe linia plan d # 952 ;;
Cel mai mic dintre unghiurile dintre liniile d și d „noi numim unghiul dintre linia și planul.
Noi Denotă ca # 966; = (d, # 952;)
În cazul în care d ⊥ # 952;. apoi (d, # 952;) = π / 2
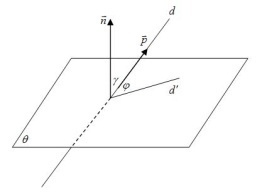
Oi → j → k → - sistem de coordonate rectangulare.
Ecuația planului:
Noi credem că punctul setat linie și vectorul direcție: d [M 0, p →]
Vectorul n → (A, B, C) ⊥ # 952;
Apoi, rămâne să se determine unghiul dintre vectorii n → și p →, ce notăm # 947; = (n →, p →).
Dacă unghiul # 947;<π/2. то искомый угол φ=π/2−γ .
Dacă unghiul # 947;> π / 2. apoi unghiul dorit # 966 = # 947; -π / 2
Apoi, unghiul dintre linia dreaptă și planul poate presupune prin formula:
Vopros29.Ponyatie formă pătratică. Sign-definiteness a formelor pătratice.
formă pătratică j (x1. X2. ..., xn) n variabile reale x1. x2. ..., xn este suma formei
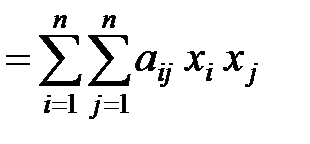
în cazul în care AIJ - unele numere, numite coeficienți. Fără a pierde din generalitate, putem presupune că aij = Aji.
Forma pătratică se numește valabilă în cazul în care aij Î GR. Matricea formei pătratice este o matrice compusă din coeficienți săi. Formularul pătratice (1) corespunde unei matrice simetrică unică
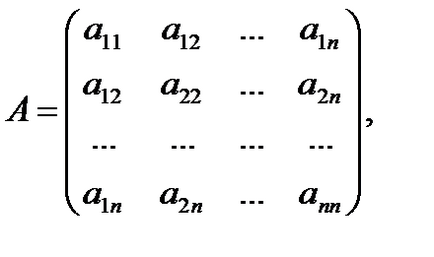
Invers, orice matrice simetrică (2) corespunde formei pătratice numai până pentru a desemna variabile.
Rangul formei pătratice se numește rangul matricei sale. Forma pătratică numita nedegenerat dacă este matricea nesingular A (reamintim că matricea A este nesingular dacă determinant său este nenul). În caz contrar, forma pătratică este degenerată.
Forma pătratică (1) este pozitiv definită (sau pozitiv puternic), dacă
A este pozitiv definită formă pătratică j (x) este, de asemenea, declarat a fi pozitiv definită. Prin urmare, forma pătratică pozitiv definită corespunde cu matrice definit numai pozitiv și vice-versa.
Forma pătratică (1) este negativă determinată (sau strict negativă) dacă
La fel ca mai sus, o formă negativă quad pătratic matrice bine definit, de asemenea, numit definit negativ.
Prin urmare, o formă definită pozitiv (negativ)-quadra Ung de j (x) atinge un minim (maxim) valorile j (x) = 0 pentru x = (0, 0, ..., 0).
Rețineți că cele mai multe dintre formele pătratice nu este un semn clar, care este, ele nu sunt nici pozitiv, nici negativ. Astfel de forme pătratice se aplică la 0, nu numai la origine, ci și în alte locații.
Când n> 2, necesită criterii speciale pentru a valida conectarea definiteness a formelor pătratice. Să le examinăm.
minori principale ale unei forme pătratice este numit un minor:
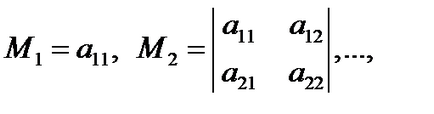
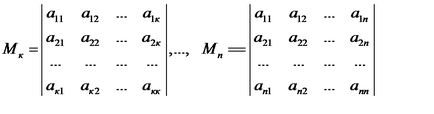
adică, este minori de ordinul 1, 2, ..., n al matricei A. situat în colțul din stânga sus, dintre care ultima coincide cu determinantul matricei A.
Criteriul definiteness pozitiv (criteriul Sylvester)
În forma pătratică j (x) = x T Ax este pozitiv definit, este necesar și suficient ca toate principali minori ai matricei A sunt pozitive, adică: M1> 0, M2> 0, ..., Mn> 0. Criteriul de certitudine negativă pentru forma pătratică j (x) = x T Ax a determinat negativ, este necesar și suficient ca principali minori sale sunt pozitive, chiar și ordine ciudat - negativ, adică M1 .. <0, M2> 0, M3 <0, …, (–1) n