valuri

C o d e r n x g și n la r și

1. Într-un E D E S E.

2. T E O R E W E T I C K I J B H O O R.

3. R ​​E W E N E W A D A B B A C T 1 și EGE - 88 W A D A Ch

3-1. m o t e m o t e h u c a m a t i n și k.

3-2. p p y g și n d m n s t o i n și k.

3-3. Râsul și n și h e c la g la circa l e b a n s.

3-4. e l e o m p r o m și n și t n e s la circa l b e a n s.

4. R E W E N E W A D A B B A C T ȘI UTILIZAREA 2-56 W A D A Ch

4-1. m o t e m o t e h u c a m a t i n și k.

4-2. p p y g și n d m n s t o i n și k.

4-3. Râsul și n și h e c la g la circa l e b a n s.

4-4. e l e o m p r o m și n și t n e s la circa l b e a n s.

5. Problema deciziilor independente - 17 sarcini.

6. T A B L E C N F O R M U L A M I.

R E W E N E W A D A B B A C T 1 și CSE

Particle suferă mișcare armonică simplă. Deplasarea x ca funcție de timp este prezentată în Figura 1. Care sunt amplitudinea, perioada, viteza maximă și accelerația maximă a acestei mișcări?

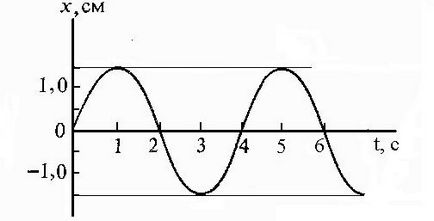
Amplitudinea este deviația maximă a unei particule din poziția de echilibru. Figura arată că aceasta corespunde celei mai mari valori deviație A = 1,5 cm. Perioada T este intervalul de timp în care există o oscilație completă a particulei. În acest caz, judecând din figura, perioada oscilațiilor T particulei = 4.

Pentru a determina valorile maxime ale vitezei și accelerației, x ecuație de scriere a particulei (t) = Asin # 969; o t. Faza inițială de oscilație a particulei, în acest caz, # 945; = 0, deoarece se mută de particule de origine. frecvență de oscilație ciclica de formula # 969; o = 2π / T = 1,57 rad / s.

Viteza particulei oscilante este prima derivata a deplasării particulei:

Viteza este, de asemenea, o funcție armonică. Expresia A # 969; o este amplitudinea acestei funcții, adică, Reprezintă maxim particulele fluctuații de viteză:

Accelerarea particulelor este prima derivata a vitezei particulelor, sau derivata a doua a deplasării particulelor:

Accelerația este, de asemenea, o funcție armonică. Expresia A # 969; O² este amplitudinea acestei funcții, adică, Este accelerația maximă a particulei

Cupru suspendat mingii de la un izvor, mișcarea de ridicare. Cum se schimbă perioada de oscilație, în cazul în care arcul atârnă de aluminiu a mingii aceeași rază?

Deoarece granulele suspendate la primăvară, sunt pendule de primăvară, perioadele de oscilație a găsit de formula:

În aceste formule, k - coeficientul de rigiditate al arcului; m1 = # 961, 1 · V - greutatea bilei de cupru, m2 = # 961; 2 · V - greutate minge aluminiu. Volumele V bile identice, așa cum sa menționat în problema că razele de bile sunt egale.

Rezultatele soluției arată că perioada de oscilație a pendulului a scăzut cu 1,8 ori.

R E W E N E W A D A B B A C T I 2 UTILIZARE

Pe o suprafață de apă plutitoare dreptunghiulară masă m bar și aria secțiunii transversale S (fig. 5). El a raportat viteza Vo călcați. îndreptată vertical în jos. Găsiți frecvență, în fază inițială și amplitudinea de oscilație a barei.

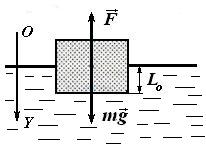
În poziția de echilibru bara este scufundat în apă la adâncimea Lo. La bar, forțe: mg - forța gravitației și flotabilitatea Arhimede F = # 961; Slo g, în cazul în care # 961; - densitatea apei. Prima lege a lui Newton se realizează, înregistrate în proiecții pe axa Y. Pe

În cazul fluctuațiilor când bara este scufundată la o adâncime de (Lo y +) crește acționează asupra blocului, flotabilitatea și bara se va deplasa în conformitate cu a doua lege a lui Newton

unde a este accelerația barei, care poate fi exprimată ca derivata a doua în raport cu timpul, prin mutarea a = y“.

Scăzând ecuația (2) Ecuația (1), obținem

Ecuația rezultată (3) este o ecuație diferențială de oscilații armonice. Solutia sa are forma

folosim condițiile inițiale pentru a determina amplitudinea și faza inițială:

Prin primăvara, capătul superior al care este fixat, agățat o greutate de m = 0,1 kg. K = constantă elastică de 40 N / m. Se determină amplitudinea oscilațiilor verticale ale sistemului, în cazul în care timpul inițial tras în jos de sarcină de echilibru poziție distanța ho = - 10 cm și comunică viteză nulă = 3,5 m / s, îndreptat în sus.

Dintre condițiile problemei sunt cunoscute masa de încărcare m și primăvară constanta k. Prin urmare, cunoscută perioadă de oscilație T a pendulului elastic și frecvența unghiulară # 969; :

Noi scriem ecuația pentru sarcină armonică oscilație x (t) = Asin (# 969; t + # 966;) și ecuația pentru vitezei de vibrație armonică V (t) = A # 969; cos (# 969; t + # 966; ).

Noi transformăm aceste condiții inițiale sunt scrise sub forma:

Noi erect expresiile obținute în piață, în jos și de a găsi amplitudinea:

Ascensorul Perioada de repaus oscilații balansoare matematice T = 0,628s. Ce accelerație și pentru a muta liftul la perioada de oscilație a coincis cu perioada de sarcină oscilație în masă m = 0,1 kg, suspendat pe o rigiditate arc k = N 12,1 / m.

Scriem expresia pentru cele trei perioade de oscilații armonice:

1) într-un pendul matematic Quiescent elevator: T = 2π√ L / g (1), unde L - lungimea firelor pendulului

2) aceeași matematică ascensorul pendul, se deplasează cu accelerație: T1 = 2π√ L / (g + a)

De la formula (1) express L = gT² / 4π² și înlocuind în (2):

gT² / 4π² = m (g + a) / k, unde se obține formula accelerare:

a = gT²k / 4π²m - g = 1,21g - g = + 2,06 m / s 2.

Semnul (+) indică faptul că accelerația și direcționată în sus.