Cum de a găsi raza
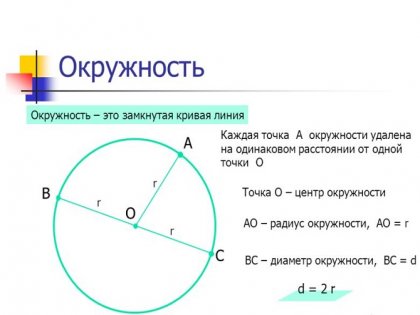
La livrarea de o varietate de examene pe elev are nevoie de cunoștințe de bază de geometrie. Prin urmare, fiecare elev trebuie să știe cum să găsească raza cercului a lungimii sale, suprafața și alte necunoscute în mai multe moduri, folosind fiecare în funcție de unele sau alte date cunoscute.
Găsirea o rază necunoscută poate fi prin parametrii geometrici: lungimea, suprafața, etc și, de asemenea, folosind cele cunoscute trei puncte care nu sunt situate pe o singură linie dreaptă, cerc, și-au stabilit coordonatele lor ...
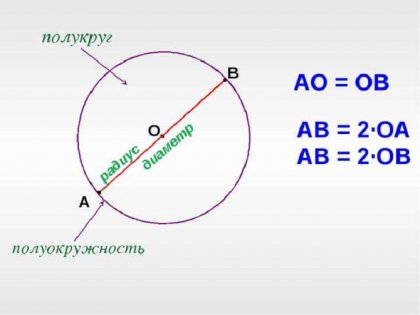
După cum se știe, raza - este orice distanta de la punctul central la punctele, care sunt amplasate direct pe cerc, prin figura centru, de asemenea, prevăzut cu diametrul. Bazat pe două determinări, raza cercului pentru a găsi doar suficient prin următoarea metodă.
Astfel, pentru a găsi raza cercului de diametru cunoscut, este necesar să se aplice următoarea formulă: r = D \ 2. In acest r expresie denotă raza necunoscută (de exemplu, în centimetri) și D - diametrul. În cazul în care diametrul cercului este numărul 64, raza va fi egală cu 32.
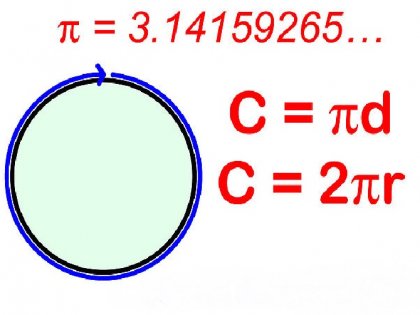
Găsiți raze de cerc suficient de ușor lungime știu circumferință - adică lungimea tuturor punctelor sale componente situate la distanță egală de centrul figurii. Pentru a găsi valoarea dorită, este necesar să se aplice următoarea formulă: C = 2πr.
In aceasta formula C este luat pentru circumferința π - constantă este „Pi“, care este egal cu valoarea 3.14 și r în problemele școlare - raza dorită. Astfel, din această formulă exprimând r, raza poate fi găsit după cum urmează: r = C \ 2π.
Evident, cu circumferință mai mare, la o considerabilă puncte distanță raza cercului mai mare.
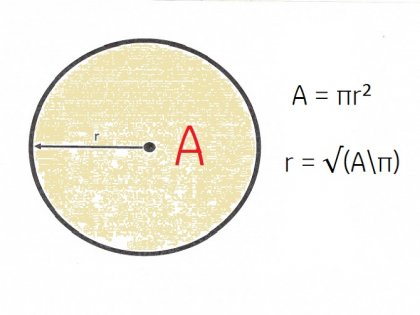
Dacă problema este cunoscută doar în zona unui cerc - adică, tot spațiul acoperit de cerc, raza cercului poate fi găsit prin următoarea formulă: A = πr2.
În formula pentru zona A este luată circumferința, π - o „pi“ constant, cu o valoare de 3,14, și r - raza dorită. Din formula de mai sus care exprimă valoarea dorită, am constatat că raza poate fi deci: r = √ (A \ π).
Astfel, folosind această formulă, o zonă cunoscută de 21 cm2 raza cercului ar fi 8,12 cm.
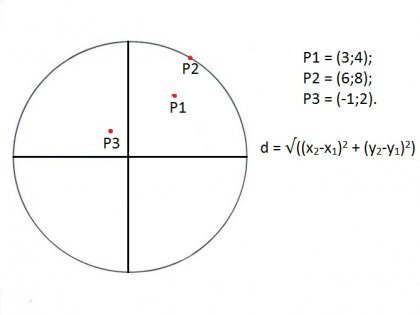
Există o teoremă a dovedit că prin aceste trei puncte care nu sunt situate pe condițiile de pe aceeași linie, este posibil să dețină un singur cerc, astfel încât să putem găsi raza cercului definit de trei puncte. Toate cele trei puncte trebuie să aibă coordonatele lor.
Centrul cercului suplimentar, care poate fi construit pentru o mai mare claritate, este calculată utilizând respectivele trei puncte, după cum urmează. Astfel, centrul figurii este situată în interiorul unui triunghi, laturile sale se calculează cu ajutorul formulei: distanța dintre două puncte; este listat în imagine.
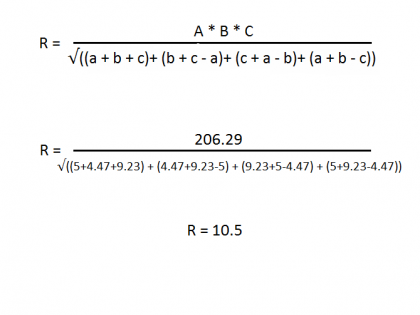
După ce se găsesc toate laturile triunghiului, este necesar să se găsească raza cercului circumscris care se calculează r = (abc) / √ ((a + b + c) + (b + c - a) + (c + a - b) + ( a + b - c)), unde a, b, c - această parte a triunghiului, și r - raza cercului dorit.
Astfel, găsirea raza se reduce la calcularea corectă a operațiunilor matematice.
9621 9622 9623 9624 9625
Pentru a găsi raza cercului, de preferință:
- determina care dintre prezentat în textul metodelor cele mai potrivite pentru situația descrisă în problema;
- utilizând această metodă pentru a efectua o acțiune este cel mai bine în mod constant și fără grabă, deoarece riscul de a face o greșeală aici este cel mai mare;
- vopsea imagini vii, condițiile corespunzătoare ale problemei, adică. a. Uneori ajută să facă o treabă bună în rezolvarea problemei (nu numai pentru a gasi cercul necunoscut).