Ecuațiile cubice sunt de forma ax 3 + bx 2 + cx + d = 0. O metodă de rezolvare a acestor ecuații este cunoscut pentru mai multe secole (a fost descoperit în matematicienii italieni din secolul al 16-lea). Rezolvarea unor ecuații cubice este destul de dificil, dar cu abordarea corectă (și un nivel bun de cunoștințe teoretice), va fi capabil să rezolve chiar și ecuațiile cubice cele mai dificile.
pași Editare
Metoda 1 de la 3:
Decizia de formula pentru a rezolva o ecuație pătratică Edit
Verificați dacă vă prezentăm o ecuație cubică constantă pe termen. După cum sa menționat mai sus, ecuațiile cubice sunt de forma ax 3 + bx 2 + cx + d = 0, unde coeficienții „b“, „c“ și „d“ poate fi egal cu 0, adică ecuația cubică poate fi compus dintr-un singur membru (i variabilă în al treilea grad). În primul rând, verificați dacă vă prezentăm o ecuație pe termen cubice constantă, adică, „d“. Dacă există un membru gratuit, puteți rezolva această ecuație cubică, folosind formula pentru rezolvarea unei ecuații pătratică.
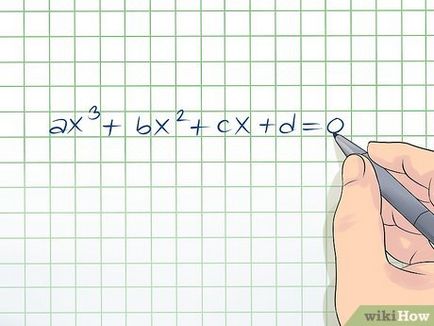
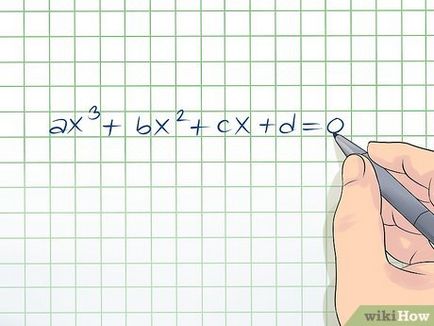
- Dacă un membru liber acolo, utilizează o altă metodă de soluție (vezi secțiunea următoare).
Deoarece în această ecuație nu există nici un termen liber, toți membrii acestei ecuații conține variabila „x“, care pot fi scoase din paranteze: x (ax 2 + bx + c).
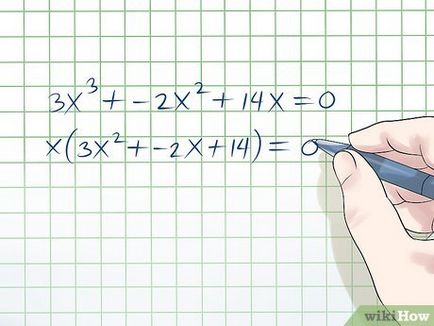
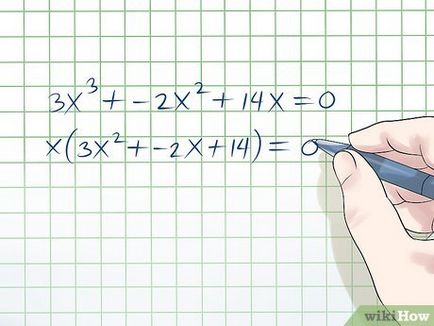
- Exemplu. 3x 3 + -2x 2 + 14x = 0. Dacă face un "x" din paranteze, veți obține x (3x 2 + -2x + 14) = 0.
Rețineți că ecuația în paranteze - această ecuație pătratică de forma ax 2 + bx + c, care pot fi rezolvate cu ajutorul formulei (b +/- √ (b 2 - 4ac)> / 2a). Rezolva ecuația de gradul doi si rezolva ecuația cubică.
- In exemplul nostru, pentru a substitui valorile coeficienților "a", "b", "c" (3, 2, 14) în formula: b +/- √ (b 2 - 4ac)> / 2a / 2 (3) / 6 / 6/6
- Soluția 1: / 6 i> / 6
- Soluția 2: i> / 6
Amintiți-vă că ecuațiile pătratice au două soluții, un cub - trei soluții. Veți găsi două soluții la pătrat, și, prin urmare, ecuația cubică. Când scoateți „x“ din paranteze, a treia soluție este întotdeauna 0.
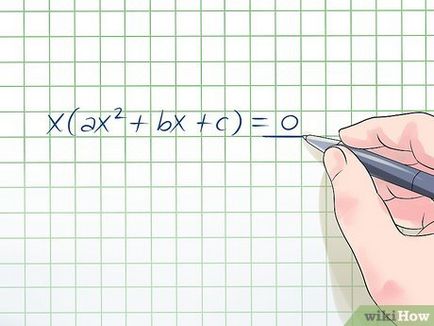
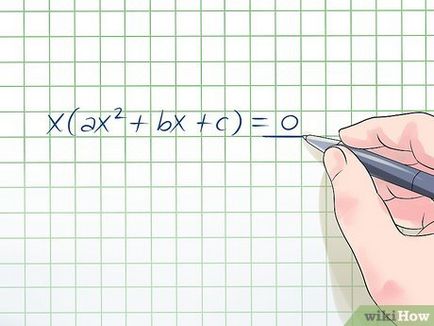
- Acest lucru este adevărat, deoarece orice număr sau expresie, înmulțit cu 0 este 0. Deci, ai scos „x“ din paranteze, vă întindeți o ecuație cubică în doi factori ( „x“ și o ecuație de gradul doi), dintre care unul trebuie să fie egale 0, astfel încât întreaga ecuație este 0.
Metoda 2 din 3:
Găsirea unor soluții întregi folosind factoring Editare
Verificați dacă vă prezentăm o ecuație cubică constantă pe termen. Sunt descrise în secțiunea anterioară, metoda nu este adecvată pentru rezolvarea ecuațiilor cubice, în care termenul liber este prezent. În acest caz, va trebui să utilizeze metoda descrisă în prezenta și secțiunile următoare.
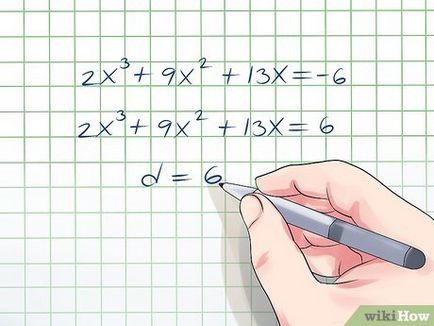
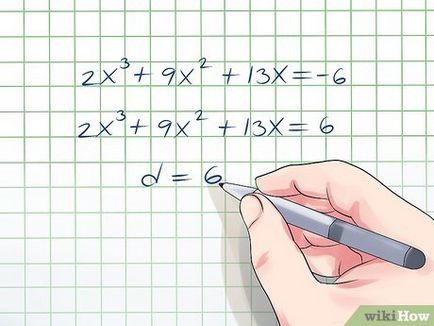
- Exemplu. 2x 3 + 9x 2 + 13x = -6. Aici transfera membru gratuit d = -6 la partea stângă a ecuației pentru a ajunge pe partea dreapta 0: 2x 3 + 9x 2 + 13x + 6 = 0.
Multiplicatorii Coeficientul de a obține „o“ (coeficient de 3 x) și constantă termenul „d“. Factori de - un număr care atunci când este multiplicată împreună dau numărul inițial. De exemplu, numărul de multiplicatori 6 sunt numerele 1, 2, 3, 6 (1 * 6 = 6 și 2 * 3 = 6).
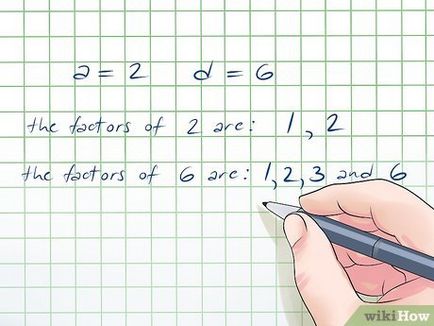
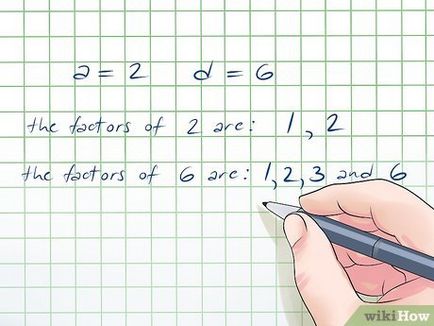
- În acest exemplu, a = 2 și d = 6. Multiplicatorii 2 - este numărul 1 și 2. Multiplicatorii 6 - este numărul 1, 2, 3 și 6.
Se împarte multiplicatorii coeficientului „și“ pe un drum liber multiplicatorilor membru „d“. Veți obține fracții și numere întregi. Întreaga soluția ecuației cubice va fi fie unul dintre aceste numere întregi, sau o valoare negativă a uneia dintre aceste numere întregi.
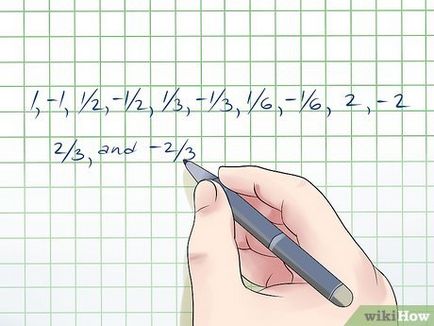
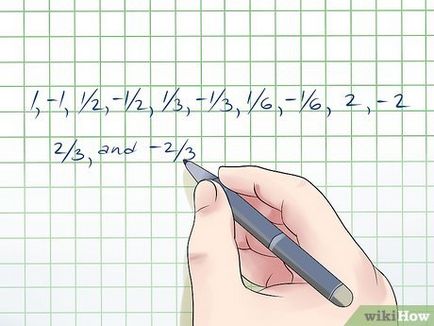
- In exemplul nostru, împărțiți factorii "o" (1, 2) privind factorii "d" (1, 2, 3, 6) și de a primi: 1, 1/2, 1/3, 1/6, 2, 2/3. Acum, se adaugă la acest interval de numere de valori negative sunt 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 , -2/3. Soluții întregi ale ecuației cubice vă aflați în această serie de numere.
Acum puteți găsi întregul soluții ale ecuației cubice, înlocuind numere întregi din setul de numere găsit. Dar, dacă nu doriți să pierdeți timpul în acest sens, vă rugăm să folosiți schema Horner diviziune. Această schemă presupune diviziunea întreg pe valorile „a“, „b“, „c“, „d“ din ecuație cubică. În cazul în care restul este 0, numărul întreg este o soluție dintr-o ecuație cubică.
- schema de Divizia Horner - un subiect dificil; Pentru mai multe informații cu privire la aceasta, faceți clic pe link-ul de mai sus. Aici este un exemplu de modul de a găsi una dintre soluțiile date pentru a vă ecuația cubică prin împărțirea schema Horner: -1 | 09 februarie 13 __ luna iunie | -2-7-6 __ | 2 7 6 0 0 Ca reziduu, apoi una dintre soluțiile este numărul întreg -1.
