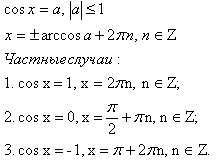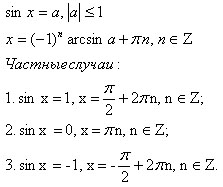Formula trigonometric, conversia trigonometrice dublei formula unghi

Raportul dintre gradul și unghiul de măsuri radian

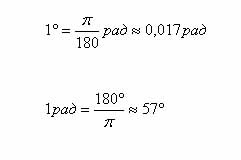
Definiții:
trigonometrice ale unghiurilor acute pot fi definite ca raportul dintre lungimile laturilor unui triunghi dreptunghic.

Sinus și cosinus unghiului determinat pentru orice unghi α. Tangenta definită pentru toate valorile unghiului a, cu excepția α = π / 2 + πn (a = 90o + 180ș * n), n = 0, +/- 1, +/- 2 cotangentă definit pentru toate valorile unghiului a, α cu excepția = πn (α = 180º * n), n = 0, +/- 1, +/- 2.

Funcția sin α. cos α, sec α cosec α și au o perioadă de 2π, iar funcțiile și tg α ctg α - o perioadă π:

sin (a + 2πn) = sin α; cosec (α + 2πn) = α cosec;

cos (α + 2πn) = cos α; sec α + 2πn) = sec α;

tg (α + πn) = tgα;

ctg (α + πn) = ctg α; n = 0, +/- 1, +/- 2.

Calcularea valorilor funcțiilor trigonometrice din orice unghi se reduce la calcularea valorilor funcțiilor trigonometrice ale unui unghi ascuțit de următoarele reguli:

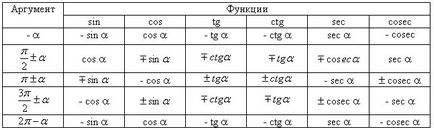
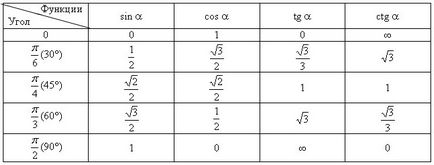
Unele dintre valorile funcțiilor trigonometrice

identitățile trigonometrice de bază

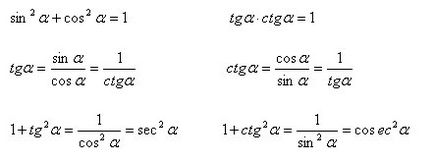
Par sau impar funcții trigonometrice

Funcția (x) F se numește chiar dacă F (-x) = F (x).
Funcția (x) F se numește ciudat dacă F (-x) = - F (x).
Funcția (x) F este numit fie un par sau impar în toate celelalte cazuri.

sin α, tg alfa, ctg alfa și cosec alfa - funcții impare.

sin (- a) = - sin alfa tg (- α) = - tg α; ctg (- α) = - α ctg; cosec (- α) = - cosec α.

cos a și sec α - chiar și funcția.

cos (- α) = cos α; sec (- α) = α sec.

funcțiile trigonometrice ale sumei și diferență de unghiuri

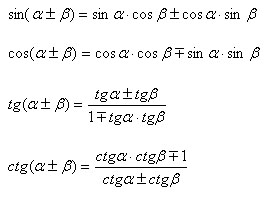
Expresia sinα, cosα, tgα prin tg (α / 2)

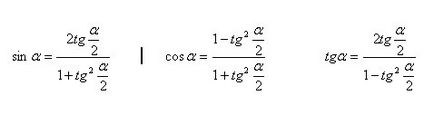
Exprimarea unor funcții trigonometrice prin intermediul altor

Funcții trigonometrice de unghiuri duble, triple și jumătate

Formulele jumătate de unghi semne în radicalii din față sunt luate în funcție de semnul funcției trigonometrice pe partea stângă.
Fiecare dintre formulele pentru tangenta și cotangentă valabile numai în condițiile în care toate valorile sale funcții există.

Conversia sumă (diferență) a trigonometric muncii funcțiilor (transformarea expresiilor trigonometrice într-o formă convenabilă pentru logaritmare).

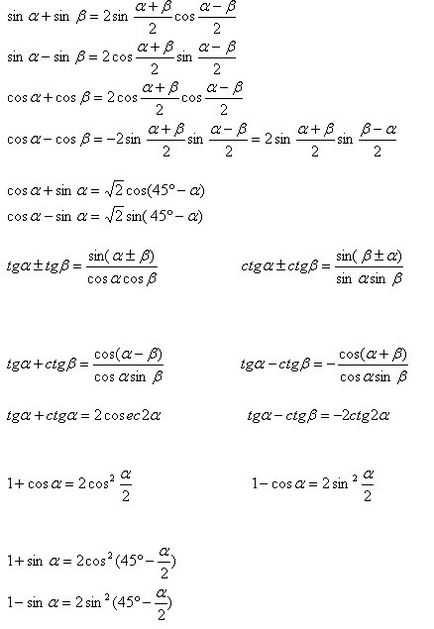
Produsele de conversie a funcțiilor trigonometrice în sumă.

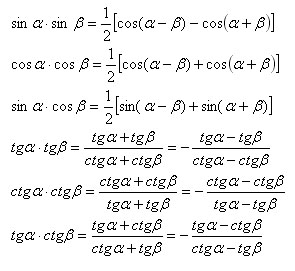
Partea dreaptă și stângă a fiecărei formule, care include tangenta și (sau) cotangentă trebuie să existe în mod simultan.

Cea mai simplă Relația dintre funcțiile trigonometrice inverse.

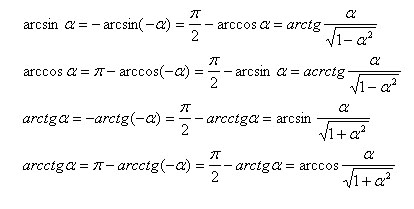
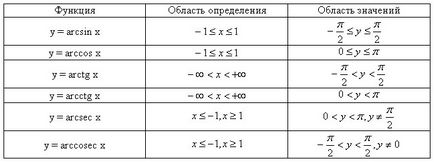
Soluție de ecuații trigonometrice.