Geometria planului (planimetrie)

hexagon regulat - Hexagon convexe, toate unghiurile a căror sunt egale și toate părțile sunt egale.

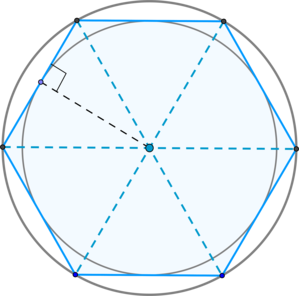
\ (\ Blacktriangleright \) Fiecare unghi al hexagonului regulat este \ (120 ^ \ Circ \).

\ (\ Blacktriangleright \) Unele dintre hexagonului regulat poate fi descris ca un cerc: raza este egală cu partea ei.

\ (\ Blacktriangleright \) diagonala mare a unui hexagon regulat împarte în \ (6 \) triunghiuri echilaterale a căror înălțime este egală cu raza cercului înscris într-un hexagon regulat.

\ (\ Blacktriangleright \), centre de inscriptionare circumscrise cercuri în jurul hexagon regulat este punctul de intersecție al diagonalelor hexagonului mare.

\ (\ Blacktriangleright \) Suprafața unui hexagon regulat cu latura \ (a \) este egal cu \ [S = \ dfrac2a ^ 2 \]

sarcina 1 <ЕГЭ

Raza cercului inscris este regulat hexagonal \ (\ sqrt \). Obține în jurul valorii de această rază a cercului hexagonal.

Prin proprietăți regulate raza hexagon \ (r \) al cercului inscris este perpendiculară trasată de la centrul unui hexagon regulat (centrul cercului inscris si circumscris) pe partea laterală a hexagonului; iar perpendiculara cade în mijlocul laturii.

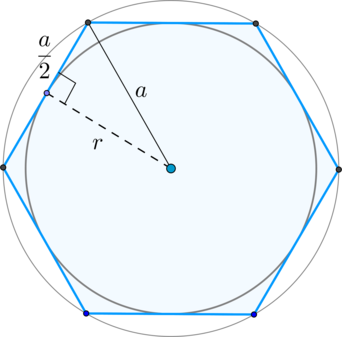
De asemenea, prin proprietatea unui hexagon regulat circumscris raza cercului este egal cu \ său lateral (a \). Apoi, din triunghiul unghi-dreapta:

\ [A ^ 2 = \ stânga (\ frac a2 \ dreapta) ^ 2 + r ^ 2 \ quad \ rightarrow \ quad a = \ dfrac 2 \, r \ quad \ rightarrow \ quad a = \ dfrac2 \ cdot \ sqrt = 4 \]

Astfel, raza cercului este egal cu \ (4 \).

sarcina 2 <ЕГЭ

Găsiți distanța dintre două laturi paralele ale unui hexagon regulat cu partea \ (\ sqrt \).

Luați în considerare hexagon regulat \ (ABCDFE \), și în ea un triunghi \ (ABC \). O pereche de laturi paralele sunt \ (AB \) și \ (DF \). \ (BC \) și \ (FE \). \ (CD \) și \ (EA \).
Nu uitați că unghiul unui hexagon regulat este egal cu \ (120 ^ \ Circ \).

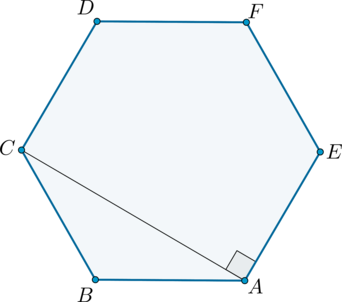
\ (\ Triangle ABC \) isoscel (\ (AB = BC \, \)), prin urmare, \ (\ angle BAC = 0,5 \ cdot (180 ^ \ ^ 120 Circ \ Circ) = 30 ^ \ Circ \ ). Astfel, \ (\ unghiul CAE = 120 ^ \ ^ 30-Circ \ = 90 ^ Circ \ Circ \).

Prin urmare, \ (AC \) - distanța dintre părțile \ (AE \) și \ (CD \) (pentru a determina distanța dintre două linii paralele - segment trase din orice punct al unei linii drepte perpendicular pe linia a doua).

Găsim \ (AC \), de regula cosinus (\ (AB = BC = o = \ sqrt \)):

\ (AC ^ 2 2 = a ^ + o ^ 2-2a ^ 2 \ cdot \ cos120 ^ \ = 2a Circ ^ 2 (1 \ cos120 ^ \ Circ) = 2 \ cdot 108 \ cdot \ stânga (1+ \ frac12 \ dreapta) = 3 \ cdot 108 \ quad \ rightarrow \)

activitatea 3 <ЕГЭ

Suprafața unui hexagon regulat este egal cu \ (24 \ sqrt3 \). Găsiți lungimea mai mare diagonală.

Prin proprietatea unui hexagon regulat de mare diagonală de două ori pe mâna lui. Prin urmare, dacă \ (AB = a \). de \ (AD = BF = CE = 2a \).

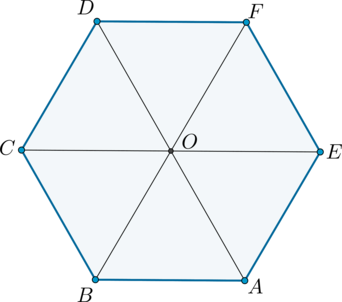
pentru că Aceste hexagon regulat diagonală împărțit în 6 triunghiuri echilaterale, suprafața fiecărui este egal cu \ (\ frac4 a ^ 2 \). suprafața totală a hexagonului este egală cu

\ [S = 6 \ cdot \ dfrac4a ^ 2 = 24 \ sqrt3 \ quad \ rightarrow \ quad a = 4 \ quad \ rightarrow \ quad AD = 2a = 8. \]

sarcina 4 <ЕГЭ

Într-un cerc circumscris în jurul hexagon regulat \ (ABCDEF \). la punctul \ (A \) a avut loc tangente. Găsiți unghiul dintre această tangentă și \ drept (AD \). Raspuns da grade.

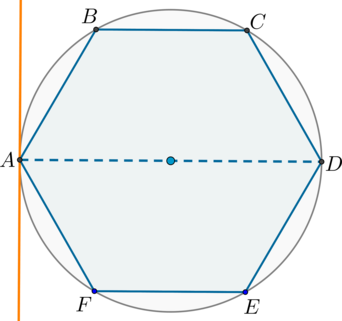
pentru că să fie centrul unui hexagon regulat în jurul cercului este punctul de intersecție al diagonalelor mari, se afla pe segmentul \ (AD \). adică \ (AD \) - diametrul cercului circumscris. pentru că Raza trasă la punctul de contact, perpendicular pe tangenta, unghiul dintre tangenta și \ (AD \) este egal cu \ (90 ^ \ Circ \).

sarcina 5 <ЕГЭ

Despre hexagon regulat \ (ABCDEF \) descrie un cerc centrat în punctul \ (O \). De câte ori zona a zonei hexagonului mai mare al unui triunghi \ (AOK \). în cazul în care \ (K \) - partea din mijloc \ (BC \).

Prin proprietatea unui circumscris hexagon regulat se află la intersecția diagonalelor mari. În consecință, \ (AO \) - raza cercului. De asemenea, prin proprietatea raza cercului este latura hexagonului regulat, astfel \ (AB = AO = x \).

pentru că \ (\ Triangle AOB \) - este corectă, \ (\ unghiul AOB = 60 ^ \ Circ \). \ (\ Triangle BOC \), este de asemenea corectă. pentru că cu condiția de \ (OK \) - mediana în dreptul \ (\ triunghi BOC \). ea și bisector, adică \ (\ unghiul BOK = \ frac12 \ cdot 60 ^ \ = 30 ^ Circ \ Circ \). Astfel, \ (\ unghiul AOK = 90 ^ \ Circ \). că este, \ (\ triunghi AOK \) - dreptunghiular.

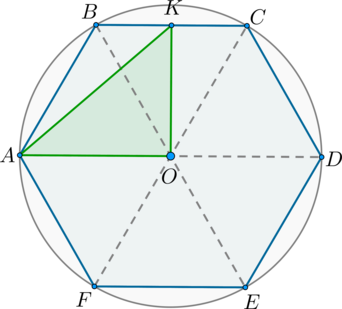
Prin urmare, \ [S _ = \ dfrac12 \ cdot AO \ cdot OK = \ dfrac x2 \ cdot OK \]

Suprafața unui hexagon regulat este egală cu suma suprafețelor de șase triunghiuri regulate:

\ [S_ = 6 \ cdot \ dfrac12 \ cdot BC \ cdot OK = 6 \ cdot \ dfrac x2 \ cdot OK \]

sarcina 6 <ЕГЭ

Despre hexagon regulat \ (ABCDEF \) descrie un cerc centrat în punctul \ (O \). Găsiți o parte mare a triunghiului \ (AOK \). unde \ (K \) - punctul de mijloc lateral \ (BC = \ sqrt7 \) hexagon \ (ABCDEF \).

Prin proprietatea unui circumscris hexagon regulat se află la intersecția diagonalelor mari. În consecință, \ (AO \) - raza cercului. De asemenea, prin proprietatea raza cercului este latura hexagonului regulat, astfel \ (AB = AO = \ sqrt7 \).

pentru că \ (\ Triangle AOB \) - este corectă, \ (\ unghiul AOB = 60 ^ \ Circ \). \ (\ Triangle BOC \), este de asemenea corectă. pentru că cu condiția de \ (OK \) - mediana în dreptul \ (\ triunghi BOC \). ea și bisector, adică \ (\ unghiul BOK = \ frac12 \ cdot 60 ^ \ = 30 ^ Circ \ Circ \). Astfel, \ (\ unghiul AOK = 90 ^ \ Circ \). că este, \ (\ triunghi AOK \) - dreptunghiular.

Prin urmare, o mare parte în \ (\ triunghi AOK \) - este ipotenuzei \ (AK \). Conform teoremei lui Pitagora a \ (\ triunghi BOK \) (\ (OK \), este, de asemenea, în înălțimea sa):

Astfel, Pitagora a \ (\ triunghi AOK \) Teorema:

sarcina 7 <ЕГЭ

Despre hexagon regulat \ (ABCDEF \) descrie un cerc centrat în punctul \ (O \). Distanța de la punctul \ (O \) la una dintre laturile sale este egal cu \ (4 \ sqrt \). Găsiți raza acestui cerc.

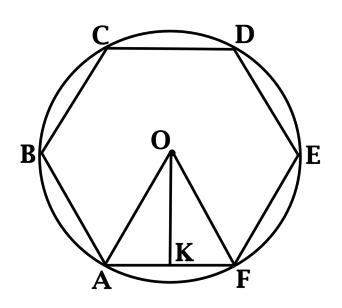
Raza cercului din jurul hexagon regulat este partea a hexagonului.

\ (OK \) - înălțimea triunghiului \ (AOF \). a redus de la \ (O \). Având în vedere că distanța de la punctul de la linia - o lungime de perpendiculara a scăzut de la acest punct de pe acea linie, apoi \ (OK = 4 \ sqrt \).
Să \ (R \) - raza cercului, în timp ce \ (OF = R \). \ (KF = 0,5R \) (din \ (OK \) Mai mult și median), astfel pitagoreic \ (R ^ 2 = (0,5R) ^ 2 + (4 \ sqrt) ^ 2 \ ). unde \ (R = 8 \).

Pe „un hexagon regulat și proprietățile sale“ la examenul la matematică este atribuită în mod tradițional, mai multe sarcini. Mai mult decât atât, în funcție de starea studentului se poate solicita ca un răspuns detaliat și scurt. Acesta este motivul pentru care, în cursul pregătirii pentru livrarea absolvenților test de calificare ar trebui să învețe cu siguranță cum să rezolve problemele în utilizarea proprietăților această cifră, în care trebuie să găsească partea ei, diagonală, raza de un cerc cu un hexagon regulat înscris, și așa mai departe. D.

Pentru a umple golurile de cunoaștere, „pompă“, abilități și de a îmbunătăți cunoștințele proprii pe această temă va ajuta proiectul educațional „Shkolkovo“. Experții noștri au pregătit și prezentat întregul material de bază pentru a se pregăti pentru examen în forma cea mai accesibilă.

Pentru a consolida cunoștințele pe care le oferim pentru a practica în rolurile lor respective. Pentru a le găsi, va fi capabil să „Catalog“ secțiune. Pentru fiecare exercițiu, site-ul prezintă un algoritm de rezolvare și răspunsul corect.

Pentru a pregăti studenții examen de la Moscova și în alte orașe sunt online. orice tip de exercițiu poate fi salvat în caz de necesitate în secțiunea „Favorite“. În viitor, această sarcină poate fi revizuit și, de exemplu, discuta algoritmul soluțiilor sale cu profesorul.

Făcând clic pe „Înregistrare“ Accept termenii Contractului de utilizator