Lecția „unghiul dintre o linie dreaptă“
Text Lecții de decodare:
Unghiul dintre drepte
Am examinat deja trei cazuri de locație directă reciprocă:
- drepte, care au doar un singur punct comun, și anume, linii se intersectează
- Liniile nu se intersectează, dar se află în același plan; Liniile sunt paralele
- Liniile nu se află într-un singur plan, și anume, linii încrucișate
Un unghi între linii intersectate denumit unghiul care nu este mai mare decât oricare dintre celelalte trei unghiuri (adică cea mai mică dintre cele patru colțuri formate).
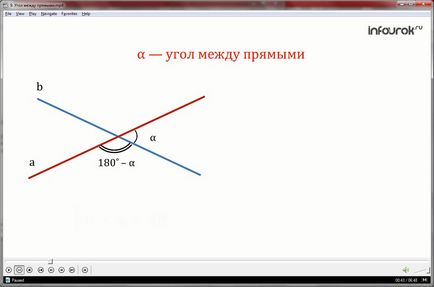
În cazul în care liniile sunt perpendiculare, valoarea unghiului dintre liniile care se intersectează va fi egală cu 90.
Prin urmare, unghiul dintre linii intersectate poate fi acută sau drepte, iar magnitudinea sa este mai mare decât 0, dar mai mică sau egală cu 90
Ne-am uitat la unghiurile dintre intersectează liniile în același plan. Încercați să determine unghiul dintre liniile oblice.
Pentru a face acest lucru, vom construi linii drepte paralele cu datele, astfel încât acestea se află în același plan. (Imagine)
Deci, pentru unghiul de linii oblice AB și CD este unghiul format prin intersectarea A₁K₁D₁ linii drepte și A₁V₁ S₁D₁ paralele AB și respectiv CD.
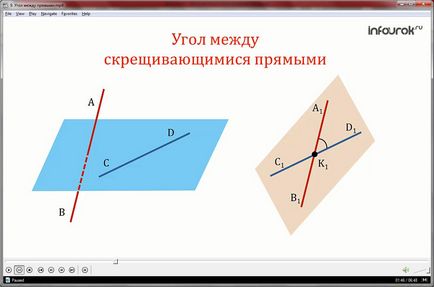
Se determină dacă valoarea A1K1D1 depinde de punctul de alegere K₁.
Notă punctul K₂ arbitrare și trage-l prin paralela directă și A₂B₂ C₂D₂ la AB și CD, respectiv.
Pe una dintre liniile, de exemplu, CD-uri să ia un punct K „și construi A'b“, care conține un punct dat.
Conform teoremei celor trei linii paralele, A₁B₁ || A₂B₂ || A'b“, din moment ce fiecare dintre ele este paralelă cu AB.
Prin teorema pe trei linii paralele C₁D₁ || C₂D₂.
În consecință A'K'D unghiurile laterale, A₁K₁D₁ A₂K₂D₂ respectiv și aceeași direcție.
Deci, A'K'D = A₁K₁D₁ = A₂K₂D₂ de teorema la colțuri cu partidele codirectional.
Astfel, după ce a analizat mai multe construcții diferite în ceea ce privește punctele K₁, K₂, K „am ajuns la concluzia că:« Magnitudinea unghiului oblic între liniile drepte din punctul de selecție este independentă»

Găsim valoarea unghiului dintre liniile oblice.
Înainte de a ne AB și CD - distorsiona linii, AB și A - care se suprapun, și A și CD - paralel.
Care este unghiul dintre liniile AB și CD în cazul în care:
Deoarece AOF = 49˚; A || CD-uri, unghiul oblic între liniile AB și CD este 49˚.
b) Dacă VOF = 104˚. unghiul dintre liniile drepte AB și CD este 76˚. Deoarece unghiul dintre liniile care se intersectează și AB mai 0˚, dar mai mic sau egal cu 90˚ și deci egală cu AOF = 180˚ - 104˚ = 76˚ proprietatea unghiurilor adiacente.
Dacă AOF = 151˚. unghiul dintre liniile drepte AB și CD este 29˚.
Prin definiție, unghiul dintre linie dreaptă nu trebuie să depășească 90 de grade, în timp ce unghiul dintre liniile intersectate și AB este 180˚ - 151˚ = 29˚, deci unghiul oblic între liniile AB și CD este 29˚.
triunghiul ACD în unghi, cu un unghi drept și C este un triunghi isoscel ABC cu o minciună de bază de curent alternativ în planuri diferite. Punctul F, K, N și M sunt punctele mediane ale laturilor AB, BC, CD și respectiv DA. ABC = 28˚, MN = ND = 3cm.
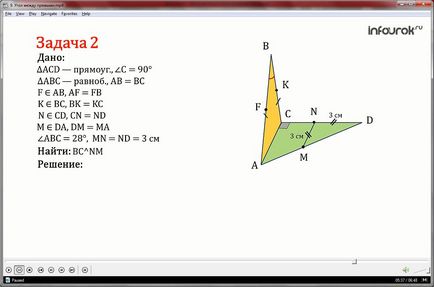
Se determină unghiul dintre liniile BC și NM, AD și FK.
Să ne amintim că în cazul în care segmentul de legătură mijlocul celor două laturi ale triunghiului, el este linia de mijloc,
Și teorema liniei medie a triunghiului este egală cu jumătate dintr-o terță parte, și paralel cu acesta.
AC direct și MN sunt paralele, ca linia de mijloc MN al triunghiului ACD.
Apoi a obține unghiul dintre BC și NM este egal cu unghiul dintre UA și NM și egal la BCA unghi.
Luați în considerare un triunghi ABC cu condiția ca este isoscel și AC baza sa, aici avem BCA unghiuri și vă sunt unghiurile la baza unui triunghi isoscel,
Din teorema sumei unghiurilor unui triunghi BCA colț exprimă este egală cu jumătate din diferența de 180 de grade și unghiul ABC.
Substituind valoarea unghiului ABC, BCA găsi unghiul este de 76 de grade
Unghiul dintre liniile BC și MN este egal cu 76 de grade.