Reducerea ecuației generale a doua comandă la forma canonică

Ecuația generală a doua suprafață comandă are forma:

Partea pătratic a ecuației - este forma pătratică

formă pătratică unei matrice:

Ecuația canonică a părții pătratic a matricei trebuie să fie diagonală. Suntem conștienți de faptul că există o transformare de coordonate ortogonale astfel încât matricea formei pătratice în noile coordonate este diagonală. Noua bază este formată din vectorii proprii

Deci, pentru a aduce ecuația generală pentru a forma canonică necesară

· Găsiți o bază ortogonală de vectorii proprii;

· Deplasarea la un nou sistem de coordonate în care matricea este o parte pătratică diagonală;

· Pentru a efectua o translație paralelă cu originea, astfel încât ecuația adoptat forma canonică (de exemplu, în centrul suprafeței superioare).

Astfel, circuitul de conducere ecuația generală de suprafață la forma canonică este aceeași ca și pentru curba. Dar există unele diferențe, de exemplu, în cazul în care valoarea proprie a formei pătratice are multiplicitatea mai mare decât 1. Să considerăm un exemplu.

Exemplu. Conduc la forma canonică a ecuației suprafeței

Găsiți sistemul de coordonate canonic.

Scriem matricea părții pătratice:

Polinomul caracteristic acestei matrice:

Rădăcinile lui sunt valorile proprii.

Cautam vectori proprii.

Pentru eigenvector este sistemul de ecuații matrice acestui sistem:

Astfel, vectorul caracteristic are o direcție normaliza său (divide cu lungimea) și să ia ca primul vector de bază nouă

Pentru vectorii proprii sunt obținute din ecuațiile matricei sistemului acestui sistem:

Astfel, vectorii proprii corespunzătoare valorii proprii 0, formează o ortogonal subspațiul bidimensional vectorului vom alege orice vector al acestui subspațiu, de exemplu normalizarea lui (divide cu lungimea) și să ia ca un al doilea vector de referință nouă Un al treilea vector bază poate fi găsit ca va aparține subspațiale vectori proprii formează o bază ortonormală în plus, orientat în mod pozitiv. Deci

Ne întoarcem la noul sistem de coordonate. Să ne amintim că vechile coordonate referitoare la noi, după cum urmează:

unde - matricea de tranziție la o nouă bază, coloanele sunt coordonatele noii vectori de bază în baza vechi.

Substitut aceste expresii în ecuația suprafeței. Partea pătratic înlocuitorului nu este necesar, în conformitate cu teorema bine cunoscută în baza vectorilor proprii ai matricei pătrat este diagonală, în cazul în care valorile proprii diagonale. Este necesar să se substituie aceste expresii numai în partea liniară:

Această ecuație este un cilindru parabolica, dar nu are canonică. Trebuie să facem o altă rotație în jurul axei ca și în plan, am ales vectorii de bază într-un mod arbitrar, dar nu erau canonice. Rotație în jurul axei definite de matricea:

Deci, trebuie să găsim un unghi. la care trebuie să facem revoluție. În general, acest lucru se face după cum urmează. avem

Deci, în cazul nostru,

După transformare ulterioară coordonate

Efectuarea traducere paralelă

și obținem în noul sistem de coordonate ecuația canonică a cilindrului parabolic:

Acum este necesar să se descrie transformarea generală de coordonate, adică exprimată prin coordonate ne amintim că matricea ortogonală inversă coincide cu transpusa. avem

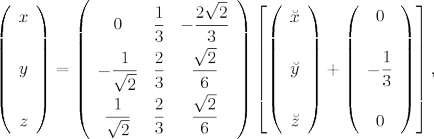
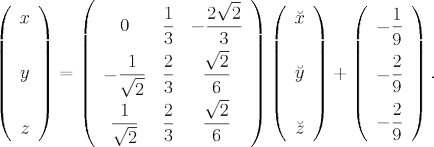
Deci, această transformare ne dă un canonic sistem de coordonate: început este la coordonatele. vectori baza noii axele de coordonate