accelerație unghiulară
Astfel, valoarea numerică a accelerației unghiulare, la un moment dat este egal cu un prim derivat al vitezei unghiulare sau derivata a doua a unghiului de rotație în timp.
Dimensiunea accelerației unghiulare a $ 1 / T ^ 2 $ ($ 1 / timp ^ 2 $); ca unitate de măsură utilizată în general $ rad / s ^ 2 $, sau, cu alte cuvinte, $ 1 / s ^ 2 $ $ (a ^) $.
Dacă viteza unghiulară modul cu timp crește, rotirea corpului este numit accelerat, iar dacă scade întârziată. Este ușor de observat că rotația va fi accelerată în cazul în care valoarea de $ \ omega $ și $ \ $ varepsilon au aceleași semne și întârziate - atunci când semne diferite.
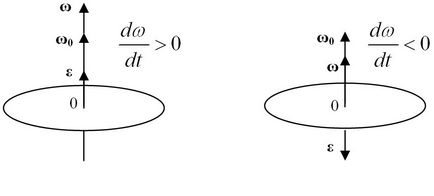
Figura 1. Vectorul accelerației unghiulare
Accelerația unghiulară a corpului poate fi reprezentat ca un vector $ \ overrightarrow = \ frac> $. direcționat de-a lungul axei de rotație. Direcție $ \ $ overrightarrow coincide cu direcția de $ \ $ overrightarrow, atunci când organismul este rotit rapid (Figura 1a), și oppositely \ $ overrightarrow \ $ în timpul rotației lente (Figura 1b).
Dacă accelerația unghiulară a corpului pe tot parcursul mișcării rămâne constantă ($$ = const), rotația se numește ravnoperemennym. Noi găsim legea ravnoperemennogo de rotație, presupunând că timpul inițial $ t_0 $ = $$ $$ unghi 0 și viteza unghiulară 0 $$ $$ = (0 $$ - viteza unghiulară inițială).
Formula $ \ varepsilon = \ frac = \ dot = \ ddot $ au d $ \ omega $ = $ \ varepsilon $ dt. Integrarea partea stângă în intervalul de \ $ omega_0 $ la $ \ omega $, precum și dreptul - în intervalul de la 0 la t, vom găsi:
$ \ Omega $ = $ \ omega_0 $ + $ \ varepsilon $ t, d $ \ varphi $ = $ \ omega $ 0dt + $ \ varepsilon TDT $.
În cazul în care valoarea de $ \ omega $ și $ \ $ varepsilon au același semn, atunci rotația va fi accelerată în mod uniform, iar dacă este diferit - ravnozamedlennym.
Accelerația unghiulară asociată completă și tangențială. Pentru punctele de rotație uniform pe un cerc de rază R, $ a _ = \ varepsilon R $. Dat fiind faptul că accelerația angulară vitezei $ a_n = ^ 2R $, pentru a obține accelerație maximă: $ a = \ sqrt + o ^ 2_n> = R \ sqrt ^ 2 + 4 ^> $. În cazul uniform accelerate mișcare $ \ omega = \ varepsilon t $, $ a_n = ^ 2R = ^ 2t ^ 2R $, $ a = R \ sqrt ^ 2 + \ varepsilon> ^ 4t ^ 4> = R \ varepsilon \ sqrt ^ 2t * 4> $
Figura 2 arată direcția de rotație a giroscoapelor (giroscop) și indică ce crește viteza sau descrește unghiular. Se specifică numărul figurii, care indică în mod corect direcția accelerației unghiulare.
Pseudo viteza unghiulară este legată de direcția de rotație a regulii mâinii drepte (șurub dreapta). Fig. 2.1 și Fig. 2.3 este îndreptată în sus în Fig. 2.2 și Fig. 2.4 - în jos.
Odată cu creșterea vitezei unghiulare increment sale, și astfel vectorul accelerației unghiulare coincide cu vectorul viteză unghiulară (figurile 1 și 4). Odată cu scăderea increment ei viteza unghiulară și, în consecință, vectorul accelerației unghiulare sunt opuse vectorul vitezei unghiulare (Fig.2 și Fig.3). În consecință, toate cifrele direcția accelerației unghiulare este corectă.
Materialul se deplasează de-a lungul unui cerc cu raza R, astfel încât dependența unghiului de rotație în timpul dat de ecuația $$ = $$ t3. Găsiți accelerația totală a punctului ca funcție de timp.
Găsiți viteza unghiulară și accelerația unghiulară a punctului:
\ [\ Omega = \ frac = 3 \ alpha t ^ 2 ;; \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ varepsilon = 6 \ alpha t \]