Panta tangentei ca panta din CSE (pagina 2)
\ (\ Blacktriangleright \) Dacă ecuația liniei date în formă de \ (> \). numărul \ (k \) se numește panta.
\ (\ Blacktriangleright \) Unghi \ (\ alpha \) panta liniei - este unghiul dintre această linie dreaptă și direcția pozitivă a axei \ (Ox \) (\ (0 \ leqslant \ alpha<180^\circ\) ), лежащий в верхней полуплоскости.
\ (\ Blacktriangleright \) Formula de bază. Linia de pantă \ (y = kx + b \) este panta acestei linii drepte:
\ [\, \ Alpha >>> \]
pentru că tangentă la graficul unei funcții - aceasta este directă, atunci acesta va returna toate acuzațiile.

Dacă \ (\ alfa<90^\circ\). то \(k>0 \);
dacă \ (\ alpha> 90 ^ \ Circ \). \ (k<0\) ;
dacă \ (\ alpha = 0 ^ \ Circ \). directorul \ (k = 0 \) (ecuația linie dreaptă este de forma \ (y = b \) și este paralelă cu axa \ (Ox \));
dacă \ (\ alpha = 90 ^ \ Circ \). ecuația liniei are forma \ (x = o \) și este perpendiculară pe axa \ (Ox \).
\ Direct (y = kx + 6 \) formează un unghi \ (\ dfrac \) radian cu direcția negativă a axei \ (Ox \). Găsiți \ (k \).
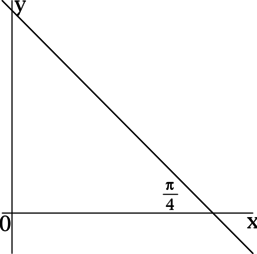
Pentru linie dreaptă dată de ecuația \ (y = kx + b \). Coeficientul \ (k \) este valoarea tangenta unghiului dintre linia \ (y = kx + b \), iar direcția pozitivă a axei \ (Ox \).
Deoarece unghiul dintre linia \ (y = kx + 6 \) și direcția negativă a axei \ (Ox \) este egal cu \ (\ dfrac \) radiani, unghiul dintre linia \ (y = kx + 6 \), iar direcția pozitivă a axei \ (Ox \) este egal cu \ (\ pi - \ dfrac = \ dfrac \) radiani, apoi \ (k = \ mathrm \, \ dfrac = -1 \).
Găsiți unghiul \ (\ alpha \) între linia dreaptă \ (y = \ sqrtx + 3 \ sqrt \) și direcția pozitivă a axei \ (Ox \). Raspuns da grade.
Pentru linie dreaptă dată de ecuația \ (y = kx + b \). Coeficientul \ (k \) este valoarea tangenta unghiului dintre linia \ (y = kx + b \), iar direcția pozitivă a axei \ (Ox \).
Astfel, \ (\ mathrm \, \ alpha = \ sqrt \). Deoarece măsura gradul unghiului dintre două linii drepte situate în intervalul \ ([0; 180 ^) \). și \ (\ mathrm \, \ alpha = \ sqrt> 0 \). de \ (0 <\alpha <\dfrac\). следовательно, \(\alpha = \mathrm\, (\sqrt) = \dfrac\). В итоге \(\alpha = 60^\) .
Sarcina 10 = examen
\ Direct (y = 21x - 6 \) formează un unghi \ (\ alpha \), cu direcția pozitivă a axei \ (Ox \). și linia \ (y = -3x \) formează un unghi \ (\ beta \), cu direcția pozitivă a axei \ (Ox \). Găsiți \ (\ mathrm \, \ alpha \ cdot \ mathrm \, \ beta \).
Pentru linie dreaptă dată de ecuația \ (y = kx + b \). Coeficientul \ (k \) este valoarea tangenta unghiului dintre linia \ (y = kx + b \), iar direcția pozitivă a axei \ (Ox \).
Astfel, \ (\ mathrm \, \ alpha = 21 \). și \ (\ mathrm \, \ beta = -3 \). Deoarece \ (\ mathrm \, \ beta \ neq 0 \). directorul \ (\ mathrm \, \ beta = \ dfrac \, \ beta> \). unde \ (\ mathrm \, \ beta = - \ dfrac \). Total: \ (\ mathrm \, \ alpha \ cdot \ mathrm \, \ beta = 21 \ cdot \ stânga (- \ dfrac \ dreapta) = -7 \).
Setarea 11 = examen
Linia dreaptă dată de ecuația \ (y = 3x + 2 \). În ceea ce privește grafica unele funcții \ (f (x) \) la punctul \ ((x_0; f (x_0)) \). și linia \ (y = 6x + 4 \) pentru graficele aceeași funcție la punctul \ ((x_1; f (x_1)) \).
Găsiți suma tangentele unghiurilor de înclinare a tangentei la graficul de \ (f (x) \) la punctele \ ((x_0; f (x_0)) \) și \ ((x_1; f (x_1)) \). în care unghiul de înclinare este considerat unghiul direct între linia dreaptă și direcția pozitivă \ (Ox \).
Pentru linie dreaptă dată de ecuația \ (y = kx + b \). Coeficientul \ (k \) este valoarea tangenta unghiului dintre linia \ (y = kx + b \), iar direcția pozitivă a axei \ (Ox \).
Astfel, pentru \ direct (y = 3x + 2 \) panta dorită egal \ (3 \). și \ direct (y = 6x + 4 \) este panta unghiul dorit \ (6 \). Total: suma tangentele unghiurilor de înclinare a tangentei la graficul de \ (f (x) \) la punctele \ ((x_0; f (x_0)) \) și \ ((x_1; f (x_1)) \) este \ (9 \ ).
Setarea 12 = examen